I am interested in the setting of differential privacy- let's say a random function $\mathcal{D}:X\to\mathbb{R}$ discriminates between (distinct) $x, y \in X$ in a differentially private way if $$ \mathbb{P}(\mathcal{D}(x) \in S) \le e^\epsilon \mathbb{P}(\mathcal{D}(y) \in S) $$ for all (Borel) subsets $S$ and also the reverse inequality holds ($\epsilon>0$ is fixed). (The prototypical example is $\mathcal{D}(x)=f(x) + $Laplace noise but I don't want the question to focus on that.)
This definition implies an upper bound on the most powerful test for $H_0:x=y$ vs. $H_A: x \neq y$ in terms of $\epsilon$ (see later in question for a naive bound). I am not familiar with the literature and would appreciate a reference for the best known bound.
In a concrete setting with Laplace noise I have estimated the max power below. For this question I am interested in general bounds with mild assumptions. On the other hand, the more work I look at this, the more I doubt much better general bounds are possible!
Edit [naive bound]: For the purposes of obtaining the bound N-P applies- after all we are just testing the distribution of $\mathcal{D}(x)$ against $\mathcal{D}(y)$.
Let's say I just test whether a single observation $o\in S$ is distributed according to $X$ ($H_0$) or $Y$ ($H_A$) and assume discreteness, for convenience of presentation. This is a N-P setting so the likelihood ratio gives the best test. $$ L(o):=\frac{\mathbb{P}(X=o)}{\mathbb{P}(Y=o)}. $$
Let the critical (rejection) region at $\alpha$ be $C$, i.e. $$ \alpha = \mathbb{P}(L(X) \in C) = \mathbb{P}(X \in L^{-1}(C)). $$ Now apply the DP definition with $S=L^{-1}(C)$ to get $$ \mathbb{P}(L(Y) \in C) = \mathbb{P}(Y \in L^{-1}(C)) \le \alpha e^\epsilon. $$
The bound derived this way for $n$ observations is
$$
\mathbb{P}(L(Y_1,\ldots,Y_n) \in C) \le \alpha e^{n \epsilon},
$$
using hopefully obvious notation.
But for $n$ and $\epsilon$s I have seen real life $\alpha e^{n\epsilon} > 1$ so the bound is useless. However, I can't see how to easily improve it. I don't mind some extra assumptions on $\mathcal{D}$, e.g. regularity or discreteness.
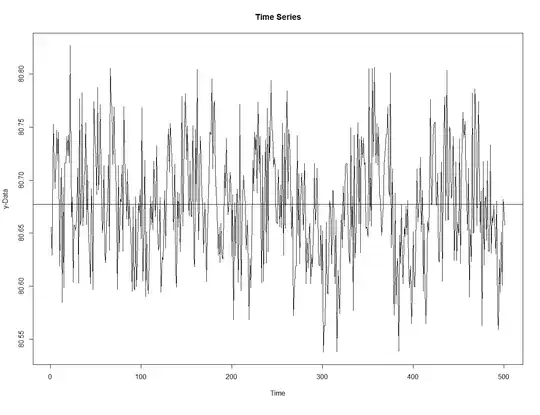
Edit2 [Comparing naive bound to actual best for $n=1$ Laplace noise] I checked the $n=1$ test explicitly with Laplacian noise (assuming parameters are known and the median differs by exactly 1, a situation that satisfies DP with scale=$1/\epsilon$). When $\epsilon$ is small (i.e. the Laplace variance is large) the log likelihood ratio is basically delta at $\pm\epsilon$ and a critical region for $\alpha < e^{-2\epsilon}/2$ does not exist. When $\epsilon$ is large the Laplace distribution is highly concentrated around its median and the critical value is around $e^{-\epsilon}$ ~$0$ and test power is ~$.5$. For moderate $\epsilon$ the bound from naive application of the DP definition is good.
So in practice the best test power looks like below ($\alpha=0.05$ and we accept using a bigger critical region for small $\epsilon$):
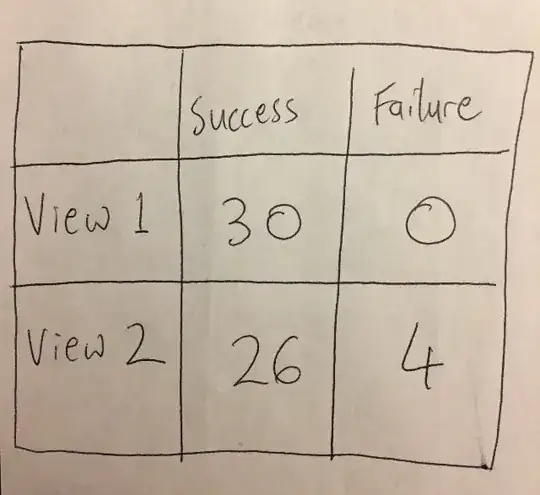
Edit3 [Naive bound is awful as $n$ increases] As the number of observations increases the naive bound becomes lousier and lousier. By $n=10$ observations it is already useless. Below power is estimated by simulation and plotted against empirical alpha$\times exp(n\epsilon)$ because an exact $0.05$ critical region doesn't exist for small alpha and epsilon.
Edit4 [Estimate max power for Laplace noise using CLT approximation to log LR]
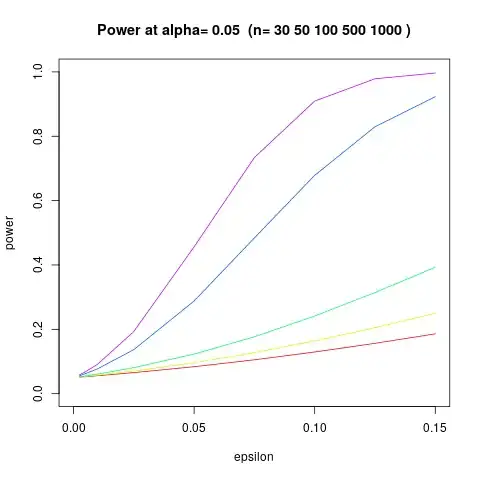
For small - moderate $\epsilon$ (s.t. the Laplace noise is reasonably flat in a neighbourhood of the median) I approximated each term in the log likelihood ratio under the null hypothesis by $$ \ln(L_i) = \begin{cases} +\epsilon & \text{w.p.} 1/2 \\ -\epsilon & \text{w.p.} e^{-\epsilon}/2 \\ U[-\epsilon,\epsilon] & \text{otherwise} \\ \end{cases} $$ and going from null to alternative hypothesis amounts to simply switching the sign (using symmetry of the Laplace distribution). This just a sum of nice distributions and the central limit theorem has already kicked in strongly around $n=30$, i.e. the null distribution is approximately Gaussian with mean $n\epsilon (1 - e^{-\epsilon})/2$ and variance given by a hideous formula. The simulation below is with $n=30$.
Using this I can estimate the power for larger $n$ (plot below). This basically answers the question for the Laplace mechanism, but I'm still interested in what can be deduced from the DP definition.