Hey I have a data set that contains hourly wind speed for about seven years. I am trying to model the data using a weibull distribution which according to literature is a good fit for hourly wind speed. However, according to the distribution I have quite a lot of zeros within my distribution. I was informed to "you will need to model zero values separately. So my first suggestion would be to try Weibull for non zero values." Anyone has any suggestions on how to go about doing this?
Asked
Active
Viewed 502 times
0
-
Basically, you model the probability of a windspeed of 0, often just by the fraction of observed windspeeds that *are* 0, and all the non-zero values get modeled by the Weibull dist'n. – jbowman Mar 29 '18 at 02:47
-
Do I separate the zeros from the non zeros or something? there 25836 zeros from a datset with 70128 data points. – L N Mar 29 '18 at 04:16
-
https://stats.stackexchange.com/questions/187824/how-to-model-non-negative-zero-inflated-continuous-data ... jbowman's suggestion is the second approach under Ben's answer there (I'd suggest it also). If you have no predictors (i.e. your model is that all observations come from the same distribution) you would rewrite your data as a column of "zero/not-0" (say recorded as 0/1) and look at the non-zero values separately (such as to fit a Weibull). If you're binning your data you may want to modify these approaches slightly. – Glen_b Mar 29 '18 at 04:16
-
1@Glen_b - good point about the binned data, I had overlooked that. When you fit the Weibull, you separate the zeros out first and only fit on the non-zero values. – jbowman Mar 29 '18 at 04:23
-
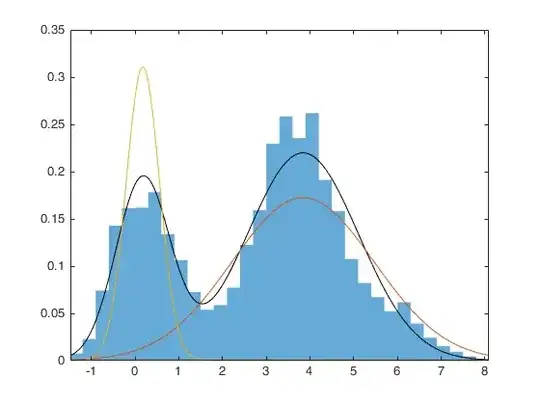
I separated the zeros and non zeros and fitted the weibull distribution to the non zeros as shown in the diagram above. Am I suppose to do anything for the zeros? – L N Mar 29 '18 at 05:20
-
Yes, you compute the proportion of them as an estimate of the probability of a zero. – Glen_b Mar 29 '18 at 05:49
-
I've closed as a duplicate because as it stands it's essentially covered by Ben Bolker's answer at the linked post and it looks like we've been doing nothing other than explaining information already there in that answer. If you want to focus on dealing with the case of binned data that might make it different enough to merit a new answer. – Glen_b Mar 29 '18 at 05:52