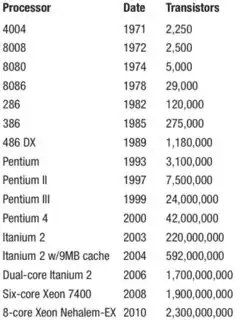
There was given some data, in which I have carry out a linearizing procedure, using either a power model or a exponential model. From my understanding, power models and exponential models are linearized virtually in the same way, except my stats professor said they were not. How am I able to differentiate between a power model and an exponential model?
Here is the data given to me: