1

This is probably a pretty simple question for most of you.

I have weekly amount of users from last 2 year till now for 2 traffic sources. Want I want to figure out is to see in which periods these sources deviate from the trend. Regarding trends I do not know which model to choose.

Since the traffic is very seasonal I don't think a standard deviation will suffice. Which trend model is best to choose here or is there a better method?

Christoph
  • 113
  • 3
  • post your data and I will try and help .. you are asking for the identification of anomalies vi Intervention Detection – IrishStat Mar 20 '18 at 21:02
  • @IrishStat thanks, I will check tomorrow if I can share it. (it's from work) is it something that I can do in a spreadsheet? Either way I will deepdive in it. – Christoph Mar 20 '18 at 21:09
  • if you can't share the real data then code it to mask the values and post a csv file – IrishStat Mar 20 '18 at 21:17
  • you can find the data below. I did a formula on all cells to mask the data (i am not sure how it's done normally), Hopefully it's usefull for you. By the way I am a marketer not a data scientist, so this is a bit new to me. https://docs.google.com/spreadsheets/d/e/2PACX-1vQSNaTHjwjHd4u0H-SDzrV-ecbw6sEqkaL8AtISfhmxqw9lZgXqm4jK6_z-5lkW1NVxdv76IdLdBeKX/pub?gid=1730495765&single=true&output=csv – Christoph Mar 21 '18 at 09:36
  • I am a little confused. Is this 128 consecutive weeks of data or is it 64 weeks of data for 2 different segs ? It appears to be 64weeks of data for two traffic sources. – IrishStat Mar 21 '18 at 10:03
  • that's correct! what I would like to do is check if both follow a certain trend and if they deviate from it at a certain point. A was looking it moving averages or maybe calculate regression maybe that's a simplier method. – Christoph Mar 21 '18 at 16:47
  • I noticed that seg2 had (roughly) similar structure ..certainly a common outlier at period 64 .. One could use the CHOW test to test the hypothesis of a common set of parameters ( seg1 vs seg2). Nothing you suggest would make any sense as nearly often simple is rong !. – IrishStat Mar 21 '18 at 17:00

1 Answers1

0

Very simple question with a not so simple answer ! In order to detect the periods that deviate from the trend one has to detect the trend in such a way that any existing deviations do not distort the identification of the trend. This is what is meant by "robust identification".

I took the 64 weekly values for segment1 and coded them withiut loss of generality for clarity. enter image description here . In order to answer your question , I need to define "trend" and "deviate from trend ... anomaly"

The general definition of what a trend is : The general course or prevailing tendency”

From http://cucis.ece.northwestern.edu/projects/DMS/publications/AnomalyDetection.pdf Anomaly detection refers to the problem of finding patterns in data that do not conform to expected behavior. These non-conforming patterns are often referred to as anomalies, outliers, discordant observations, exceptions, aberrations, surprises, peculiarities or contaminants in different application domains. Of these, anomalies and outliers are two terms used most commonly in the context of anomaly detection; sometimes interchangeably.

I took your 64 values and using simultaneous identification strategies as I discussed here How to determine order of sarima? , I obtained the following useful equation presenting regular behavior (arima structure) and the empirically identified deviant structure (pulses). enter image description here . The Actual/Fit and Forecast (not asked for) is here 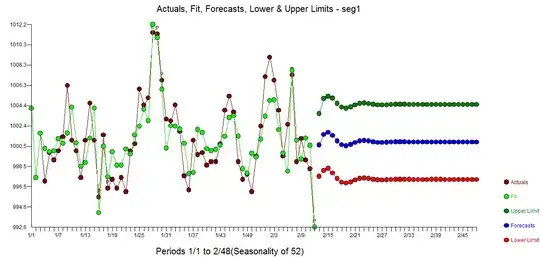enter image description here with a very clear rendition of the "deviate from normal" here 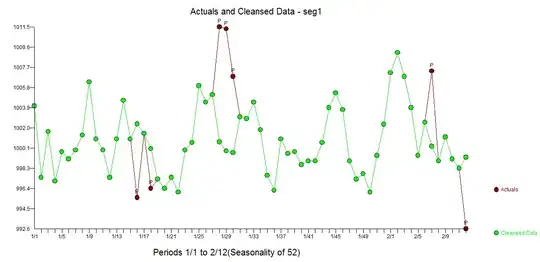enter image description here . The residuals from the model suggest sufficiency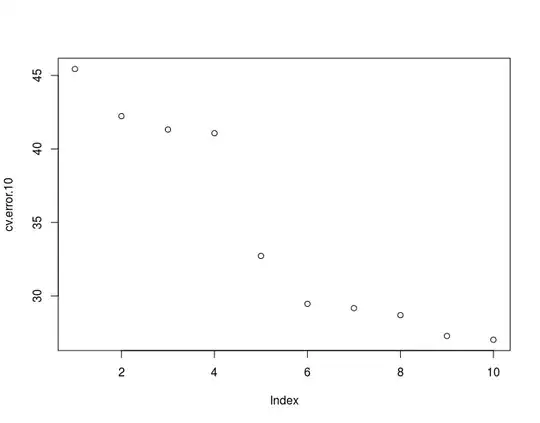 enter image description here

An ARIMA model is simply a weighted average.It answers the double question: How many period (k)should I use to compute a weighted average and precisely what are the k weights. It answers the maiden's prayer to determine how to adjust to previous values (and previous values ALONE) in order to project the series (which is really being caused by unspecified causal variables). Thus an ARIMA model is a poor man's causal model .

in our case the "trend component" is a simple two period weighted average (k=2) of the past using the most recent value and the value three periods ago. The weights are 56.1% and -34.2% and a constant 781.864 enter image description here shown for period 65. Note that in this form the prediction equation includes a slight adjustment due to the anomaly/pulse at period 64.

Hope this helps ...

By the way , my non-invasive coding of your submitted numbers was 1) subtract 2620000000 and then 2) divide by 1000 .... enter image description here ... 64 numbers/values is to brief/short to validly identify/model seasonal structure although one could assume a model perhaps auto-regressive (seasonal arima) or seasonally deterministic (weekly dummies).

IrishStat
  • 27,906
  • 5
  • 29
  • 55