Let's say there is a die. Getting an even number has a probability of $P(even)=2/9$ for each even number and $P(odd)= 1/9$ for each odd number. Let's say that $Y = F_X(x)$. Now we wish to plot $F_Y(y)$. If $X$ was continuous, then it would be $F_Y(y) = y$, but since $X$ is discrete, $F_Y(y)$ is a step function where $F_Y(y) \le y$ for all $0 < y < 1$ and $F_Y(y) < y$ for some $0<y<1$.
$F_Y(y)$
This is quite easy to see if plotted:
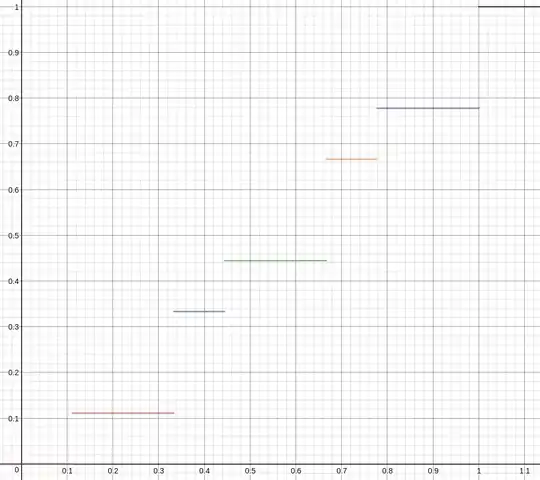
My problem is I'm not sure how to express this CDF in a mathematical way. So far I have:
$$F_Y(y) = \begin{cases} y, & \text{ if $F_X^{-1}(y) \in X$} \\ ?, & \end{cases} $$