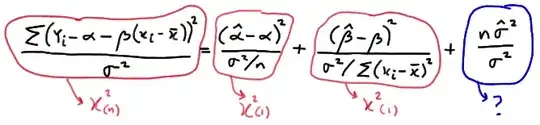I am told that, under the assumptions of the simple linear regression model, $\dfrac{n\hat\sigma^2}{\sigma^2} \sim \chi^2_{(n - 2)}$. Why is $\dfrac{n\hat\sigma^2}{\sigma^2}$ a chi-square random variable with $n - 2$ degrees of freedom? It seems like it resembles the sum of $n$ squared standard normal variables of the form $\dfrac{\hat\sigma^2}{\sigma^2}$, so my previous knowledge leads me to think that it should have $n$ degrees of freedom? Although, I'm not convinced that it is a squared standard normal variable, since it does not totally resemble the form $\left( \dfrac{X - \bar{X}}{\sigma} \right)^2$.
My question stems from this image:
From this page.
Since the other terms take the form of a squared standard normal variable, I understand why they are chi-squared random variables with 1 degree of freedom. However, I do not understand why the last term has $n - 2$ degrees of freedom.
I would greatly appreciate it if people could please take the time to clarify this.