0

I have a PC1-PC2 plot generated by applying PCA to the combination of 2 sets of samples where red means one set and blue means the other set.

I can see that the two sets of samples are very different since each makes a clear cluster, but is it possible that this PCA plot, having crossing clouds, tells (roughly) anything about the structure of the difference between the two sets?

enter image description here

user5054
  • 1,259
  • 3
  • 13
  • 31
  • PC1 and PC2 are orthogonal within the combined data set, by construction. However, within separate datasets, they are correlated. What does this mean to you? I will think of a visual picture with pen an paper how this is possible – Chamberlain Mbah Mar 15 '18 at 11:03
  • This does not really mean anything to me.. Any suggestions? – user5054 Mar 18 '18 at 06:17
  • This popped up in the question feed as an unresolved question. I do have a couple of queries, but appreciate much time has passed and you may no longer be interested or have the answers. The original commenters made an error, PC eigenvectors are what are uncorrelated by definition, PC scores however can exhibit correlation. Was the PCA model created on both red and blue or is it an external model? If it was the two colors it may be related to Simpsons paradox (groups can artificially create correlations) but in reverse, here we may be seeing groups masking correlations to the PCA. – ReneBt Oct 13 '21 at 16:57

1 Answers1

0

Suppose, you're dealing with interest rates. There you have the yield curve, which is represented by rates from 3 months to 30 years. The rates can be pulled for today here at Fed's web side. If you draw the rates as a line with the tenor on the x-axis and the rate on the y-axis, you get a curve for each observation day, something like this one: 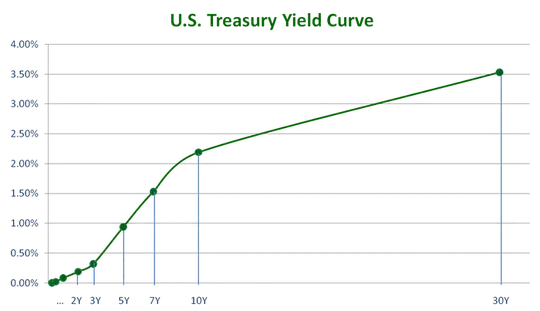enter image description here

You can observe that short rates are lower than long maturity rates on the chart above, e.g. 2 year rate is 0.25% and 30 year rate is about 3.5%. So, we can say that the yield curve is upward sloping. It's usually this way.

Now, you can collect all these curves for many days, then apply PCA like in this question. Here, each interest rate (tenor) such as 2Y, 3Y, 5Y etc. is a feature of the curve. In this case the obtained principal components will have nice interpretation: PC1 is the level of the yield curve and PC2 is its slope. You can think of a level as an average interest rate.

If you apply the loading from this PCA to your two sets, then your plot would tell the following: when the level of the curves went up, the red set had the curves flattening, while the blue set had curves steepening. Here's how you get to say this: PC1 is negatively correlated with PC2 in a red set. So, when PC1 increase it indicates that the level increases, but this tends to decrease the slope which is represented by PC2. In your case PC1 and PC2 will have a different interpretation. So, you'll have to apply this logic to your case taking into account that.

What's peculiar with your chart is that your PC1 and PC2 are correlated in these sets. The PCs are supposed to be uncorrelated. So, this is something else you need to contemplate: perhaps both your sets are different from the original sample on which you calculated the PCA loadings.

Aksakal
  • 55,939
  • 5
  • 90
  • 176
  • Thanks for the reply. What are the features (variables) on which you apply PCA in that yield example? Also, what is the "level" of a curve mean? More importantly, how would you end ups deciding that "PC1 is the level of the yield curve and PC2 is its slope"? – user5054 Mar 14 '18 at 22:21
  • You see how 5y rate is 1% that is the feature of a curve. The level is overall level of rates – Aksakal Mar 14 '18 at 22:46
  • Each yield (or product) is a sample, and each time point is a feature? – user5054 Mar 14 '18 at 22:58