0

I am attempting to test some sets of data for normality. I have 64 groups to test. Each group has n=8 samples. [[I am aware of the problems with low n in regard to normality testing]]

My end goal is to be able to test these groups against one another with a t.test() (or similar) to determine if they are significantly different from one another.

As an example from one of the groups:

x=(-82.13 -77.00 -76.80 -75.35 -74.88 -74.65 -70.93 -70.61)

To start with I have used a shapiro-wilk test (shapiro.test()) and received p value 0.462 >0.05, and W = 0.923 (I cannot reject the null hypothesis that this data is from a normal distb). I have also created histograms of each groups data.

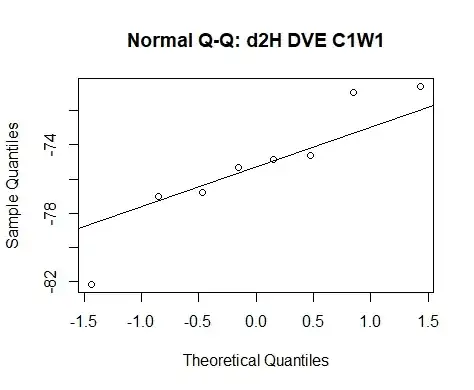
Then I use qqplot(x) and qqline(x) and get this result: QQ-plot version 1

This method/approach is what I commonly find when reading how to carry out QQ-plots online.

However, I was taught a different method in my stats class. The following is the code for the alternative method:

v.h.c1w1Data <- sort(v.w1c1h) #Sort samples
v.h.c1w1Rank <- seq(1:length(v.w1c1h)) #Provide rank for each data point  
v.h.c1w1F <- v.h.c1w1Rank/(length(v.w1c1h)+1) #Calculate the empirical prblty.    
v.h.c1w1Mean <- mean(v.w1c1h)    
v.h.c1w1Std <- sd(v.w1c1h)     
v.h.c1w1Var <- var(v.w1c1h)    
v.h.c1w1Model <- qnorm(v.h.c1w1F,v.h.c1w1Mean,v.h.c1w1Std) #calculate mdl prblty
qqplot(v.h.c1w1Data,v.h.c1w1Model, main= "Normal Q-Q: d2H DVE C1W1",xlab="d2H data (permil)", ylab="d2H modelled")
abline(0,1)

The result is the following plot. QQ-plot v2

My Question is: Since the 2 plots are clearly different and I think would be interpreted differently, which method is appropriate and why?

Stefan
  • 4,977
  • 1
  • 18
  • 38
archemeides
  • 1
  • On the notion of testing samples for normality before applying the t-test, see [this answer](https://stats.stackexchange.com/questions/2492/is-normality-testing-essentially-useless/2501#2501) and also the relevant reference mentioned in [this answer](https://stats.stackexchange.com/questions/121852/how-to-choose-between-t-test-or-non-parametric-test-e-g-wilcoxon-in-small-sampl/123389#123389) – Glen_b Mar 09 '18 at 23:46
  • You seem to have too few data points to be testing for normality. Maybe use some robust method? – kjetil b halvorsen Mar 10 '18 at 11:21
  • Up to a change of scale and switching the axes, your plots are identical. You use different procedures for drawing a reference line: see the help page for `qqline` for the explanation. – whuber Mar 10 '18 at 19:32
  • Thanks @whuber for pointing that out, foolish of me to not have realized that :S – archemeides Mar 10 '18 at 21:09

1 Answers1

0

You should be able to look at these samples directly using qqnorm(). Here is the following example is modified from the R manual, with some annotation:

 y <- rt(200, df = 5)
 qqnorm(y); qqline(y, col = 2) ### no tranformation needed
Daniel
  • 275
  • 2
  • 7