2

I played around with the t-SNE implementation in scikit-learn and found that increasing perplexity seemed to always result in a torus/circle. I couldn't find any mentions about this in literature. Check out some examples below, which is just a slight change to sk-learn's t-sne perplexity example. I would love to learn why.

t-sne perplexity

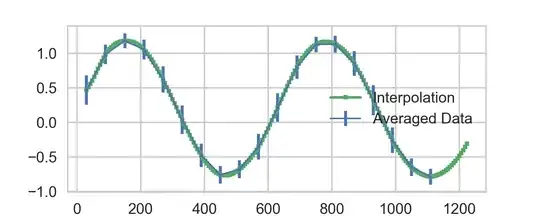
Following input from @amoeba I made a couple of extra examples with perplexity closer to the sample size of 300: enter image description here

amoeba
  • 93,463
  • 28
  • 275
  • 317
Mathias Andersen
  • 145
  • 6
  • 1
    What is the sample size here? Linked scikit code uses n=300, and you can't use perplexity larger than n: it's not possible to achieve it. Some tsne implementations will not allow it at all. – amoeba Mar 08 '18 at 11:27
  • I see. n is 300 in these examples as well. – Mathias Andersen Mar 08 '18 at 12:57
  • Then I am surprised that scikit-learn allows to run t-sne with this parameter at all. I might add this as an answer a bit later today. – amoeba Mar 08 '18 at 14:10

1 Answers1

3

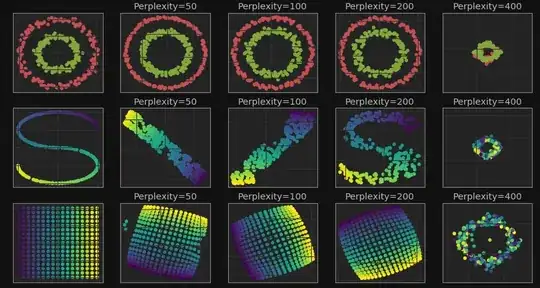
One cannot have perplexity values larger than sample size. [I don't have time right now, but I will try to provide a brief mathematical explanation of this later.]

A popular t-SNE tutorial https://distill.pub/2016/misread-tsne/ says

The image for perplexity 100, with merged clusters, illustrates a pitfall: for the algorithm to operate properly, the perplexity really should be smaller than the number of points. Implementations can give unexpected behavior otherwise.

As explained by Laurens van der Maaten, https://github.com/distillpub/post--misread-tsne/issues/2:

I just had one small remark: you show some results with perplexity 100 that are a complete mess. This mess is likely not due to a property of the algorithm, but due to the implementation you used not catching invalid parameter inputs. Note that the perplexity of a distribution over N items can never be higher then N (in this case, the distribution is uniform). For t-SNE this means you need at least 101 points to be able to use perplexity 100. If you use a perplexity setting that is too high for the number of points (and have no assertion checking for that), the binary search for the right bandwidth will fail and the algorithm produces garbage (depending on the exact implementation).

By the way, I don't trust scikit-learn implementation of t-SNE. I had various problems with it, and I prefer to use Laurens van der Maaten's C++ library (you can find Python wrappers).

amoeba
  • 93,463
  • 28
  • 275
  • 317
  • Cool, thanks. If this behavior is isolated to sk-learn and using a too high perplexity is mathematically incorrect, then I accept your answer. – Mathias Andersen Mar 12 '18 at 09:50