The solution is straightforward but messy using a standard formula, such as obtained in the first half of the Wikipedia derivation. The interest lies in simplifying the work.
I propose starting with a seemingly strange expression for the uniform distribution on the square $[a,b]\times [c,d],$ where (to avoid wrangling too heavily with negative numbers and special cases) I will assume all endpoints are non-negative. Its density is equal to $$f(x,y; a,b,c,d)=\frac{1}{(b-a)(d-c)}$$ throughout this square--that is, provided $a\le x\le b$ and $c\le y\le d$--and otherwise is zero. I will write that more formally and rigorously in the form
$$f(x,y;a,b,c,d) = \frac{1}{(b-a)(d-c)}\left[\mathcal{I}_{a,c}(x,y) - \mathcal{I}_{a,d}(x,y) - \mathcal{I}_{b,c}(x,y) + \mathcal{I}_{c,d}(x,y)\right]$$
where $\mathcal{I}$ is the indicator function of the quadrant bounded at the lower left by the point $(u,v),$
$$\mathcal{I}_{u,v}(x,y) = \left\{\array{
1 & \text{if}\quad x\ge u, y\ge v \\ 0 & \text{otherwise.}
}\right.$$
(For motivation, please see the illustrations and discussion under "Intuition from Geometry" at https://stats.stackexchange.com/a/43075/919, which uses the same idea to compute sums of uniform variables.)
To find the chance that $xy \le z$ for any $z$ all we need to do is integrate expressions of the form
$$F_{u,v}(z) = \int_{x y \le z} \mathcal{I}_{u,v}(x,y) dx dy.$$
These are elementary to compute. If $z\le uv$, this integral must be zero; otherwise, it is
$$\int_{x y \le z} \mathcal{I}_{u,v}(x,y) dx dy = \int_u^{\frac{z}{v}} \left(\frac{z}{x} - v\right) dx dy = z(\log(z) - \log(u) - \log(v)) - z + u v.$$
Therefore
$$\eqalign{\Pr(xy \le z) &= \int_{x y \le z}f(x,y;a,b,c,d) dx dy \\
&= \frac{F_{a,c}(z) - F_{a,d}(z) - F_{b,c}(z) + F_{c,d}(z)}{(b-a)(d-c)}.}$$
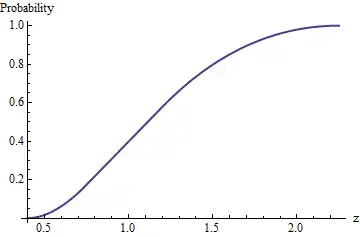
For instance, here is a Mathematica implementation of the basic integral (here written g):
g[z_, a_, b_] := Boole[z >= a b] (a b - z + z (Log[z] - Log[a] - Log[b]))
To illustrate its use, we may plot the CDF:
With[{a = 8/10, b = 3/2, c = 1/2, d = 3/2},
Plot[(g[z, a,c] - g[z, a,d] - g[z, b,c] + g[z, b,d] )/((b-a)(d-c)), {z, a c, b d}]]