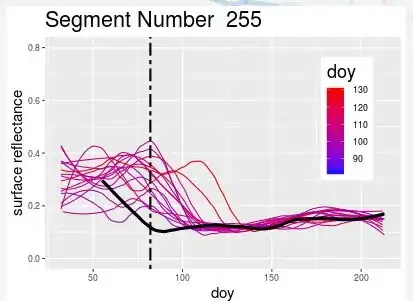
I have two different types of time series. The first group of series is much more bimodal, and the second group is much flatter. For a given time series, I want to test whether it more likely belongs with the first group or the second group. I don't really care about the specific values of the time series. It is the shape of the time series that matters and how much of a difference there is between the higher part of the series and the lower part of the series. Are there any specific tests for this? I think ARIMA modeling requires a stationary timeseries, which these are not.
Ones that look like this:
And ones that look like this: