0

I defined the distance between each observation and its centroid by:

dist=sum((X[,i]-Y[,j])^2)
# X is a 2*n observations matrix, Y is a 2*k centroids matrix
# n is the number of observations

Then I created a variable energy which represents the sum of dist for all observations.

I did that for k varying from 1 to 20 and I got these graphs: (It is energy vs. k)

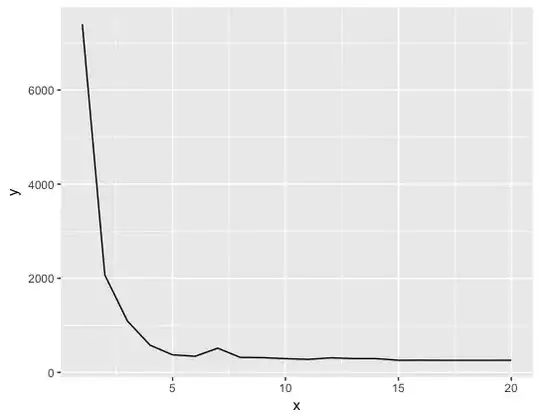
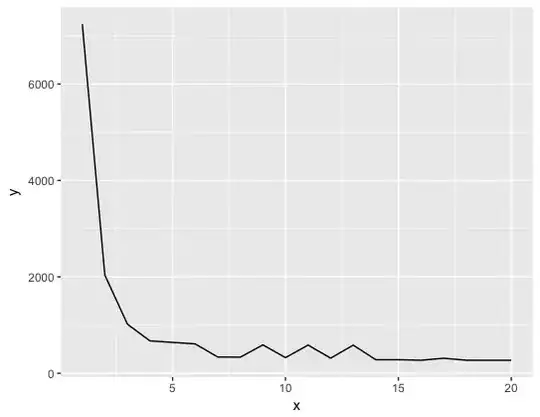
Why increasing k can increase the sum of squared residuals?

Danica
  • 21,852
  • 1
  • 59
  • 115
Louis Ansuez
  • 23
  • 3
  • Your axes are labeled x and y, but you say x and y are the data points and centroids. What do the plots represent; is it energy vs. k? Also, a nice feature of the site is that you can embed images directly into your post by clicking the image button (no need to link to external image hosting sites). – user20160 Mar 03 '18 at 23:22
  • You are right, it is energy vs k. I edited my post, thank you. – Louis Ansuez Mar 03 '18 at 23:30
  • What you're seeing is most likely the result of suboptimal solutions, as @CarlRynegardh pointed out. Just to add one more point, the true error must decrease monotonically with $k$. – user20160 Mar 03 '18 at 23:39
  • K-means is a non-deterministic algorithm; it is quite possible for this to occur. If you run it 20 or 30 times and average the results for each $K$, this effect will typically disappear or at least get much smaller. – jbowman Mar 04 '18 at 01:42

1 Answers1

3

I will assume that the plot shows the sum of within distances of k-means. That is the sum of distances of every point to their closest cluster center. The optimization of K-Means does not guarantee a global minimum. You are much more likely to find local minima. As you increase k you might be unlucky and find a bad one. You could use a smart initialization strategy like k-means++, or run k-means several times with random initalizations for the cluster centers for each k and pick the solution with lowest within cost. Using a smart initialization strategy will also speed up the computations and make you converge to the solution faster.

The results of K-Means is dependent on the cluster initialization.

Carl Rynegardh
  • 211
  • 1
  • 8