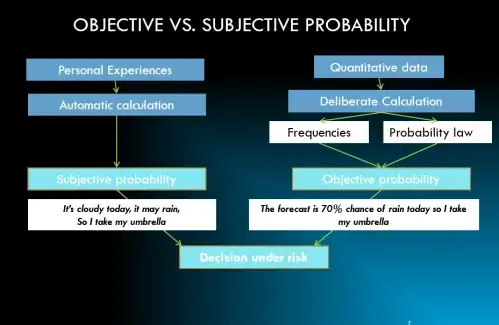
This is what I found on the web without half-trying: Subjective probability is a probability derived from an individual's personal judgment about whether a specific outcome is likely to occur.
A simple, if not especially good example of Subjective Probability
In a scenario in which a person is asked to predict the percentage chance of whether a flipped coin will land with heads or tails up, his initial response may be the mathematically true 50%. If 10 coin flips occur, all resulting in the coin landing tails up, the person may change his percentage chance to a number other than 50%, such as saying the chance of it landing tails up is 75%. Even though he knows the new 75% tails prediction is mathematically inaccurate, the individual’s personal experience of the previous 10 coin flips has created a situation in which he may choose to use subjective probability.
EDIT: As mentioned above, there is a good link for this provided by @Tim How exactly do Bayesians define (or interpret?) probability?. The view that is most commonly associated with Bayesian statistics is subjectivist view, also known as personalistic probability.
The objectivist view, A.K.A. frequentist view is that with infinite data, probability exists as an objective phenomenon with the Black Swan argument often cited as a demonstration of the non-computability of the probability of the consequential rare events using scientific methods (owing to the very nature of small probabilities).
Another example "Not all probability is objectively strictly quantifiable. Premise: “Some X are F and x is X”. Conclusion: “x is F”. The objectivist can only say “The probability (given the premises) the conclusion is true is greater than 0 but less than or equal to 1.” This is because the logical “some” implies “at least some and perhaps all.”
The subjectivist is free to say, for example, “The probability (given the premises and my beliefs) the conclusion is true is 42.8%.” But he does so only by some mysterious introspection which, in effect, adds to or subtracts from the fixed premises. Of course, most subjectivists in practice would agree with the objectivist."