I have a regression model which uses macroeconomic variables as independent variables. In running the Philips-Perron test in SAS, I get output under three different heads - Zero Mean, Single Mean and Trend as shown below:
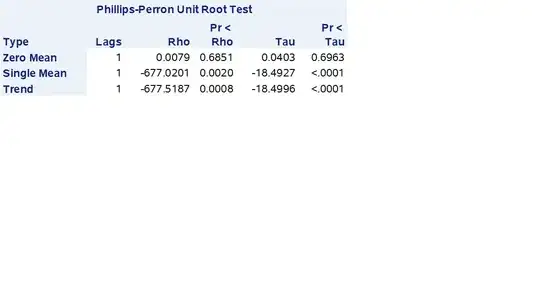
The p-value shows that my variable Y is Single Mean stationary but not Zero Mean stationary. I want to know what the difference between Single and Zero Mean stationary is - is it just that the series reverts to a mean of zero if Zero mean stationary is satisfied versus a non-zero mean otherwise? If this is the case, then can I go ahead and use variable Y if my regression model has a non-zero intercept?
Thanks for any advice!