1

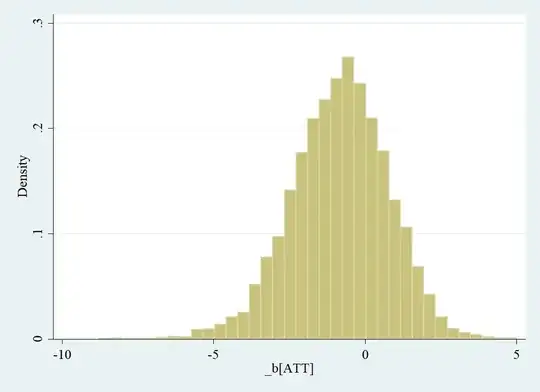
I am using propensity score matching with kernel matching to test for the average treatment effect on the treated.

enter image description here

The distribution of the bootstrapped differences is as follows:

enter image description here

I transformed them with the mean (as described in this CV -answer) and the SD to obtain z-scores. Afterwards, I counted how many observations (in abs. values) exceeded the 95% threshold of 1.65.

However, with this approach I get a p-value of 0.09.

How does this work with a (as in my case) skewed distribution?

If I simply count the observations exceeding the 2.5% and 97.5% seperately, then I obtain a summed p-value of 0.04 which is in line with the BCa confidence interval. Would this be a valid alternative?

dtribus
  • 31
  • 4

1 Answers1

1

Bootstrapping Regression Models in R An Appendix to An R Companion to Applied Regression, Second Edition goes over a lot of this pretty well.

They suggest using the confidence interval directly for hypothesis testing where possible (then you don't have to worry about the p-value).

Of the intervals you used, the BCa confidence interval has the smallest coverage error when the bootstrapped distribution of the parameter is skewed.

If your sampling distribution is normal then all the intervals you used would be the same. (see also Bootstrap confidence intervals: when, which, what? A practical guide for medical statisticians)

As a statistician, I would report the interval that best reflects the $\alpha$-level you are using (the least coverage error). However, I am sure there are many journals, etc that would prefer seeing all your intervals.

This CV question and this ResearchGate deal with creating a hypothesis test and p-value that agrees with the BCa interval.

Michael Webb
  • 1,936
  • 10
  • 21
  • Thank you for your answer! I also found this formal solution on [statalist](https://www.stata.com/statalist/archive/2011-11/msg00692.html) where a subtraction of the bias from the point estimate (ATT in my case) is suggested. However, I am a bit confused about this bias term. I know that it represents the shift/bias in the bootstrap sample. But, do I have do consider it for the overall effect? In other words, do I have to report -2.69 or the bias-corrected -4.56 (observed coefficient - bias) as the treatment effect in my results? – dtribus Feb 20 '18 at 17:07
  • From what I have seen, the effect is not adjusted for bias (but I'd be interested in cases/disciplines where it is), only the interval is. – Michael Webb Feb 20 '18 at 17:20