Suppose I wish to regress $Y$ against a normalized $X$, but I would like a sparse solution. After regression, why is discarding the coefficients with smallest magnitude not allowed?
For the record, I have heard of, and often use, LARS and LASSO methods. I'm just curious why the above approach is not applicable.
There would be no problem if $X$ were orthonormal. However, the possibility of strong correlation among the explanatory variables should give us pause.
When you consider the geometric interpretation of least-squares regression, counterexamples are easy to come by. Take $X_1$ to have, say, almost normally distributed coefficients and $X_2$ to be almost parallel to it. Let $X_3$ be orthogonal to the plane generated by $X_1$ and $X_2$. We can envision a $Y$ that is principally in the $X_3$ direction, yet is displaced a relatively tiny amount from the origin in the $X_1,X_2$ plane. Because $X_1$ and $X_2$ are nearly parallel, its components in that plane might both have large coefficients, causing us to drop $X_3$, which would be a huge mistake.
The geometry can be recreated with a simulation, such as is carried out by these R calculations:
set.seed(17)
x1 <- rnorm(100) # Some nice values, close to standardized
x2 <- rnorm(100) * 0.01 + x1 # Almost parallel to x1
x3 <- rnorm(100) # Likely almost orthogonal to x1 and x2
e <- rnorm(100) * 0.005 # Some tiny errors, just for fun (and realism)
y <- x1 - x2 + x3 * 0.1 + e
summary(lm(y ~ x1 + x2 + x3)) # The full model
summary(lm(y ~ x1 + x2)) # The reduced ("sparse") model
The variances of the $X_i$ are close enough to $1$ that we can inspect the coefficients of the fits as proxies for the standardized coefficients. In the full model the coefficients are 0.99, -0.99, and 0.1 (all highly significant), with the smallest (by far) associated with $X_3$, by design. The residual standard error is 0.00498. In the reduced ("sparse") model the residual standard error, at 0.09803, is $20$ times greater: a huge increase, reflecting the loss of almost all information about $Y$ from dropping the variable with the smallest standardized coefficient. The $R^2$ has dropped from $0.9975$ almost to zero. Neither coefficient is significant at better than the $0.38$ level.
The scatterplot matrix reveals all:
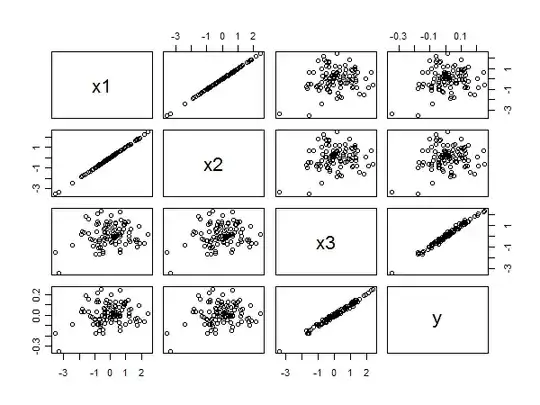
The strong correlation between $x_3$ and $y$ is clear from the linear alignments of points in the lower right. The poor correlation between $x_1$ and $y$ and $x_2$ and $y$ is equally clear from the circular scatter in the other panels. Nevertheless, the smallest standardized coefficient belongs to $x_3$ rather than to $x_1$ or $x_2$.
Seems to me that if an estimated coefficient is near 0 and the data is normalized that prediction would not be hurt by discarding the variable. Certainly if the coefficient was not statistically significant there would seem to be no problem. But this must be done carefully.The IVs may be correlated and removing one could change the coefficients of others. This gets more dangerous if you start reoving several variables this way. Subset selection procedures are designed to avoid such problems and use sensible criteria for including and excluding variables. If you ask Frank Harrell he would be against stepwise procedures. You mention LARS and LASSO which are two very modern methods. But there are plenty of others Including information criteria that peanlize the introduction of too many variables.
If you try a subset selection procedure that has been carefully studied with a lot of literature about it you will probably find that it will lead to a solution that reoves variables with small coefficients especially if they fail the test for being statistically significantly different from 0.
