The max-stability property of the GEV distribution is quite well known
in relation with the Fisher-Tippett-Gnedenko theorem. The GPD has the
following remarkable property which can be named threshold
stability and relates to the Pickands-Balkema-de Haan theorem. It
helps to understand the relation between the location $\mu$ and the
scale $\sigma$.
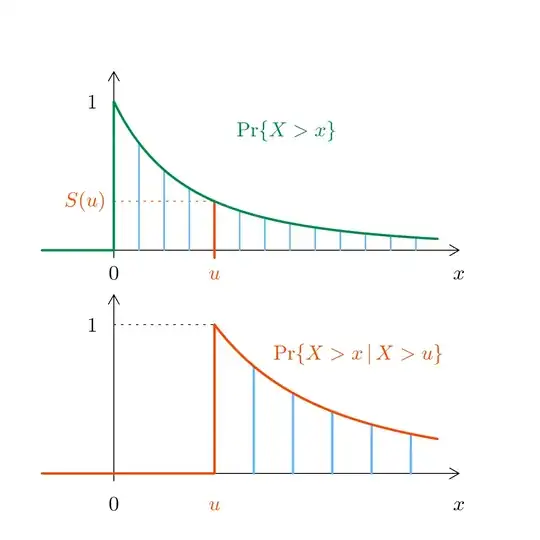
Assume that $X \sim \text{GPD}(0,\,\sigma,\,\xi)$, and let $\omega$ be
the upper end-point. Then for each threshold $u \in [0,\, \omega)$,
the distribution of the excess $X-u$ conditional on the exceedance
$X>u$ is the same, up to a scaling factor, as the
distribution of $X$
\begin{equation}
\tag{1}
X - u \, \vert \, X > u \quad \overset{\text{dist}}{=} \quad a(u) X
\end{equation}
where $a(u) = 1+ \xi u / \sigma> 0$. So, conditional on $X >u$, the
excess $X-u$ is GPD with location $0$ and shape
$\sigma_u := a(u) \times \sigma = \sigma + \xi u$.
An appealing interpretation is when $X$ is the lifetime of an item. If
the item is alive at time $u$, then the property tells that it will
behave as if it was a new one and if the time clock was changed with
the new unit $1 / a(u)$. See Figure, where a positive value of $\xi$ is used,
implying a rejuvenation and a thick tail.
It seems that in most applications of the GPD the parameter $\mu$ is
fixed, and is not estimated. The scale parameter $\sigma$ should then
be thought of as related to $\mu$ because the tail remains identical
when $\sigma^\star := \sigma - \xi \mu$ is constant.
The relation (1) writes as a
functional equation for the survival function $S(x) := \text{Pr}\{X >
x\}$
\begin{equation}
\tag{2}
\frac{S(x + u)}{S(u)} = S[x/a(u)] \quad \text{for all }u, \, x
\text{ with } u \in [0,\,\omega) \text{ and } x \geq 0.
\end{equation}
Interestingly, the functional equation (2) nearly characterises the GPD
survival. Consider a continuous probability distribution on
$\mathbb{R}$ with end-points $0$ and $\omega >0$ possibly
infinite. Assume that the survival function $S(x)$ is strictly
decreasing and smooth enough on $[0, \,\omega)$. If (2) holds for a
function $a(u) > 0$ which is smooth enough on $[0,\,\omega)$, then
$S(x)$ must be the survival function of a
$\text{GPD}(0, \, \sigma,\,\xi)$.
 Picture 2.
Picture 2.
 Picture 3.
Picture 3.

