How does a multivariate mixed CDF look like?

Question

If I have multiple CDFs $X_1,X_2,\cdots,X_n$, (for simplicity I assume 2 : $X,Y$) and if $X$ is discrete and $Y$ is continuous, how would the joint CDF look like?

I understand that:

If they were both discrete, it would be a staircase in 2 dimensions. Similar to stacking books atop each other on a table.
If they were both continuous, it would be a nice smooth graph coming to 1 at $(\infty,\infty)$

It sounds like you are talking about the CDF rather than the PDF. — Neil G, Jul 23 '12 at 21:01
http://stats.stackexchange.com/questions/23/finding-the-pdf-given-the-cdf — whuber, Jul 23 '12 at 21:10
@whuber. I am using PDF (caps) for Cumulative and pdf (small) for the usual. — , Jul 23 '12 at 21:15
Inquest, because you are in a small minority who uses this convention, I have edited your question so it will be understood by others as you intended it. (+1 for an interesting question.) — whuber, Jul 23 '12 at 21:18

score 5 · Accepted Answer · edited Jul 24 '12 at 15:31

You've actually already put together all the right pieces in your question. The cdf is

along one axis, say $x$, a staircase (similar to stacking books atop each other on a table)
along the other axis, say $y$, continuous

So, imagine a staircase where each step has its own continuous curve, and each successive step's curve is greater than or equal to the last step's curve at every point.

Or, looking at it from the perpendicular direction, each part of a continuous curve has a corresponding staircase, each staircase greater than or equal to the last at every point.

As you say, the cdf goes to 1 as $x$ and $y$ go to $(\infty, \infty)$.

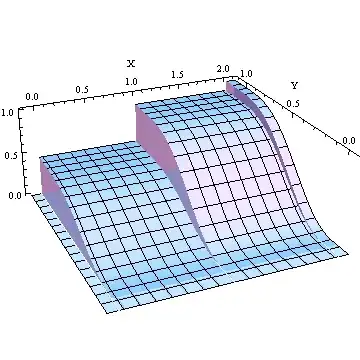
Hopefully, someone will plot such a graph…

This plot of a multivariate CDF is for a Binomial($1/3$,$2$) variable $X$ and an independent Beta$(3,4)$ variable $Y$. Because the variables are independent this CDF is the product of the individual CDFs.

@whuber: Wow, nice diagram!! (Thanks for adding it!) – Neil G Jul 24 '12 at 21:31 — Neil G, Jul 24 '12 at 21:31

How does a multivariate mixed CDF look like?

1 Answers1