Whitening/Decorrelation - why does it work?

Question

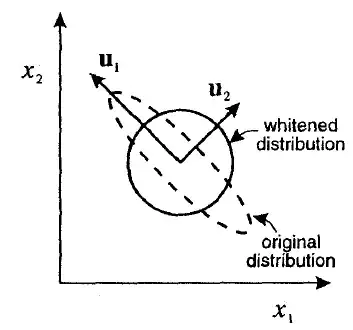
Given some whitening transform, we change some vectors $\textbf{x}$, where features are correlated, into some vector $\textbf{y}$, where components are uncorrelated. Then we run some learning algorithm on the transformed vectors $y$.

Why does this work? In the original space we had correlation between vector components, and it carried some information (correlation IS information, right?). Now, we whiten data and get a round blob as output. All information about correlation lost - to me seems like a large part of information lost. Wouldn't it be much easier to learn decision boundaries/distributions defined over correlated data (since ALL information present)? So, how does SVM (since in my practice this is the method that requires this most), for example, gives a better result with whitening?

Answer 1

Whitening is par for the course in computer vision applications, and may help a variety of machine learning algorithms converge to an optimal solution, beyond SVMs. (More on that towards the end of my answer.)

Now, we whiten data and get a round blob as output.

To put that more mathematically, whitening transforms a distribution using its eigenvectors $\boldsymbol{u}_j$ in such a way that its covariance matrix becomes the unit matrix. Bishop (1995) pp. 300 illustrates this in a stylised manner:

Whitening is a useful preprocessing step because it both decorrelates and normalises the inputs.

Decorrelation

The training step of machine learning algorithms is simply an optimisation problem, however it is defined. Whitening gives nice optimisation properties to the input variables, causing such optimisation steps to converge faster. The mechanism for this improvement is that it affects the condition number of the Hessian in steepest descent-style optimisation algorithms. Here are some sources for further reading:

• Maurya's answer on Quora
• Smith - Conditioning and Hessians in analytical and numerical optimisation: Some illustrations

Normalisation

The fact that input variables now have unit variance is an example of feature normalisation, which is a prerequisite for many ML algorithms. Indeed, SVMs (along with regularized linear regression and neural networks) requires that features be normalised to work effectively, so whitening may be improving your SVMs' performance significantly thanks only to the feature normalisation effect.