8

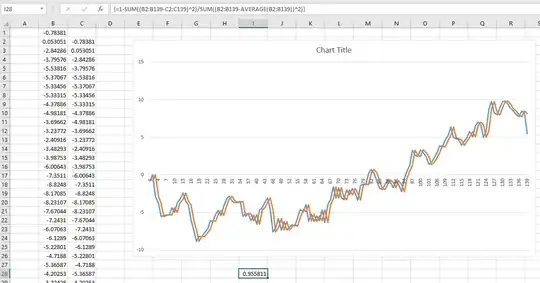
I recently came across a fascinating article about predicting future stock market returns. The author presents the graph below and cites an R^2 of 0.913. This would make the author's method far superior to anything I have ever seen on the subject (most argue that the stock market is unpredictable).

enter image description here

The author describes his method in great detail and provides substantial theory to back up the results. Then I read a second, critiquing article that referenced this paper: The Myth of Long-Horizon Predictability. Apparently people have been falling for this illusion for decades. Unfortunately, I don't really understand the paper.

This leads me to the following questions:

  • Does the false confidence of long-term predictions arise due to using the same data set for both training and model validation? Would the problem go away if training and validation data were pulled from separate, non-overlapping time periods?
  • Aside from validating on the training set, why does this problem become more pronounced over longer horizons?
  • In general, how can I overcome this problem when training models that must make long-term predictions?
Ryan Zotti
  • 5,927
  • 6
  • 29
  • 33
  • 1
    Not sure if you came across this thread on CV, where I referenced a couple of papers on this topic. https://stats.stackexchange.com/questions/294489/is-autocorrelation-in-a-supervised-learning-dataset-a-problem/294991#294991 – horaceT Feb 01 '18 at 00:00

2 Answers2

4

I think a simple answer is that one doesn't want to measure R^2 on original scale of the timeseries. If one's forecast is purely a copy of the last seen timeseries value, the R^2 would be huge. Example:

enter image description here

This could be called a spurious case. I am getting the value 0.96, while this forecast is totally bullshit-ish.

R^2 is going to give an honest value if it has been measured using stationary timeseires, for example, first differences of y and y-hat.

Alexey Burnakov
  • 2,469
  • 11
  • 23
1

The problem does not arise because we are using the same dataset for training and validation. It arises because of the effect of the persistence of the variables on magnifying sampling errors and small effects at longer time horizons. As stated in the article, even if you cannot predict future stock market returns from your variable of interest, we expect $R^2$ as well as regression coefficients to be roughly proportional to the time horizon if the variables are persistent. This is because (pg. 1584):

a) any unusual draw from the returns at time $t$ will influence the returns for $k$ periods, where $k$ is the time horizon.

b) a persistant regressor will have very similar values for $t$, $t-1$, $t-2$, .., $t-k$

and thus "The impact of the unusual draw will be roughly $k$ times larger in the long-horizon regression than in the one-period regression." In the linked article citing the very high $R^2$, the time horizon is ten years, data is available quarterly, so a time horizon of 10 years (time horizon $k = 40$) the inflation in $R^2$ will likely be very substantial.

Chris Novak
  • 845
  • 6
  • 17