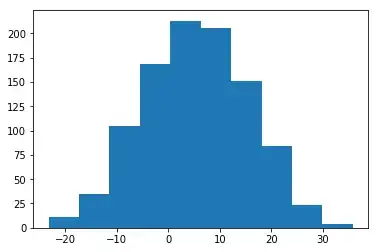
This is a very simple example, I'm simulating normally distributed data in Python, and performing a Kolmogorov - Smirnov Test on my sample to check the goodness-of-fit(of the sample distribution compared with a Normal distribution)
Code:
from matplotlib import pyplot as plt
import numpy as np
from scipy import stats
data = stats.norm.rvs(5, 10, size=1000)
plt.hist(data)
print(stats.kstest(data, 'norm'))
KstestResult(statistic=0.57991242997450898, pvalue=0.0)
However, the p-value I get is very small!-> which means I have to reject the Null hypothesis, and conclude that the sample does not follow the distribution.
Could someone explain what I'm doing wrong here?