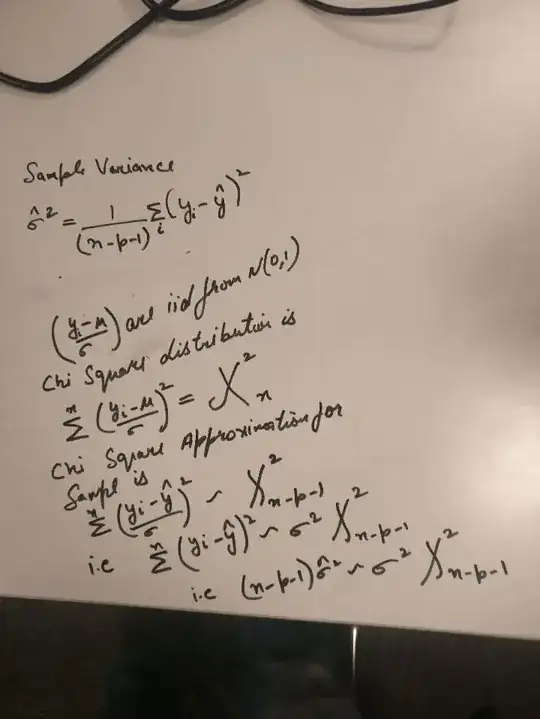In Element of statistical learning in equation 3.11, distribution of (sum of prediction error's) are approximated to actual error variance * chi square distribution of N-p-1 degree of freedom. Can you please explain how this approximation happened.
Asked
Active
Viewed 315 times
1 Answers
-1
I think I understood how this approximation worked.
the approximation from DF(n) to DF(n-p-1) is from cochran's theorem explained here where n is number of samples and (p+1) is number of features.
Paras Malik
- 9
- 3
-
The value $n-p-1$ makes a magical appearance when the DF for the chi-squared distribution suddenly changes from $n$ to $n-p-1$. I don't think anybody would find this enlightening or convincing without further explanation. – whuber Feb 02 '18 at 19:18
-
DF changed from n to n-p-1 because we are using Sample mean instead of population mean. here n is number of samples and (p+1) number of features. if we have only 1 feature then DF = n-1 for approximation. This approximation is from Cochran's theorem and better explained [here](https://stats.stackexchange.com/questions/121662/why-is-the-sampling-distribution-of-variance-a-chi-squared-distribution) – Paras Malik Feb 03 '18 at 08:04
-
Understood: but the DF doesn't magically change from one equation to the next. When you changed "$\chi^2_n$ to "$\chi^2_{n-p-1}$" you failed to change "$\sigma$" in the denominator of the left hand side to "$\hat \sigma$". – whuber Feb 03 '18 at 13:15
-
It should be σ only. Explained [here](https://en.wikipedia.org/wiki/Cochran%27s_theorem#Sample_mean_and_sample_variance) and [here](https://en.wikipedia.org/wiki/Cochran%27s_theorem#Distributions) – Paras Malik Feb 04 '18 at 03:12