Gradient Bandit Algorithm baseline

Question

I am reading Sutton's latest draft of "Reinforcement learning, an introduction" and I came to the Gradient Bandit Algorithm (page 29). I am having a bit of trouble understanding how the baseline should be computed. The book says:

"$\bar{R_t} ∈ \mathbb{R}$ is the average of all the rewards up through and including time $t$, which can be computed incrementally as described in Section 2.4 "

Section 2.4 explains briefly how to compute sample averages incrementally by using this formula: $Q_{n+1} = Q_{n+1} + (R_n - Q_n)/n$. So I am using it to compute the average reward, but I am not getting the results displayed in the book.

These are the books results:

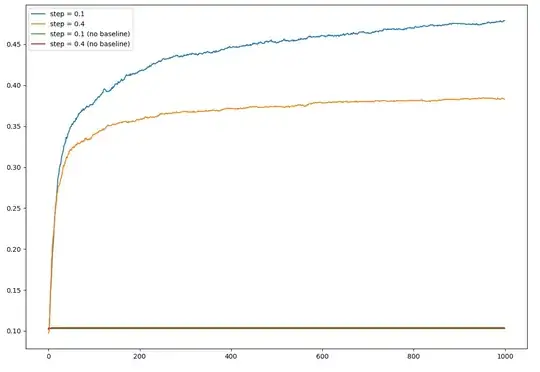
These are mine:

This is my code [it is concise, I promise :)]:

def GradientBandit(bandits, iterations, step_size, no_baseline=False):
    k = len(bandits)
    H = np.zeros(k)
    P = np.ones(k) / k
    N = np.zeros(k)

    is_optimal = np.zeros(iterations)
    avg_reward = 0
    for t in range(1, iterations + 1):
        A = np.argmax(P)

        R = bandits.reward(A)
        avg_reward = avg_reward + (1.0 / t) * (R - avg_reward)
        baseline = 0.0 if no_baseline else avg_reward

        H[A] = H[A] + step_size * (R - baseline) * (1 - P[A])
        for a in range(k):
            if a != A:
                H[a] = H[a] - step_size * (R - baseline) * P[a]


        aux_exp = np.exp(H)
        P = aux_exp / np.sum(aux_exp)
        is_optimal[t - 1] = int(bandits.is_optimal(A)) * 1.0


    return P, is_optimal

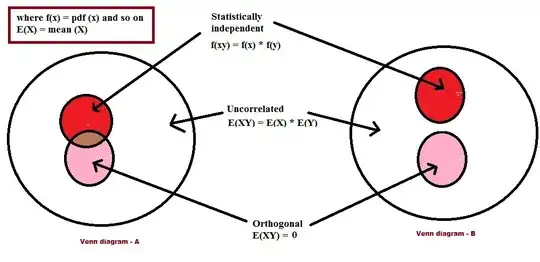
I am not sure if I misunderstood the way the baseline is supposed to be computed... At first I thought it may be a baseline per action, but then in the formula proof they state that the baseline must not depend on the selected action in order to derive the gradient correctly. Am I wrong?.

My results are pretty bad in two ways: first, the no base line algorithm is not learning anything. Second, it barely reaches like 47% in the optimal action, whereas the book results get over 80%.

The bandits testbed is a 10-bandit problem where the true expected reward is shifted 4 units as suggested in chapter 2 (this is: set the mean of each bandit = gaussian(mean=4)). The results are averages of 2000 runs with 1000 steps. The is_optimal check returns true if the action is equal to the maximum mean of all bandits.

score 7 · Accepted Answer · answered Jan 26 '18 at 21:51

7

Your implementation is very close to being correct. The issue is in the definition of $\pi$ (which you have as $P$ in your code). From the notes:

where here we have also introduced a useful new notation, $\pi_t(a)$, for the probability of taking action $a$ at time $t$.

But in your code, you take an argmax:

    A = np.argmax(P)

This should instead be a random integer with mass function defined by $P$.

answered Jan 26 '18 at 21:51

combo

1,177
7
19

4

That was the trick!. Makes sense to allow learning in the early stages of the no-baseline version. For completeness sake, this is the updated code: A = np.random.choice(k, 1, p=P)[0] – bones.felipe Jan 29 '18 at 08:38

Gradient Bandit Algorithm baseline

1 Answers1