I am working on a study of fire propagation risk, and I have estimated a generalized linear model. Looking at the resulting ANOVA, I have seen that the proportion between the model sum of squares and the total sum of squares does not match the $R$-squared terms displayed in the model output. The ANOVA is:
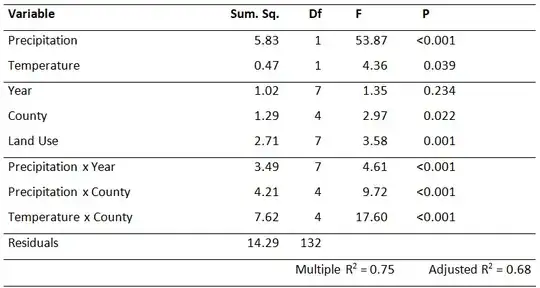 If I have calculated it correctly, the $R$-squared term should be:
If I have calculated it correctly, the $R$-squared term should be:
$R^{2} = \frac{\text{Model SS}}{\text{Total SS}} = \frac{26.64}{40.93} = 0.65$
I am also unsure about what the result should be expected (0.75 as in the multiple $R^{2}$, or 0.68)?
Do you know why this sum does not match with the $R$-squared that I computed from the table? Possibly am I confusing concepts?