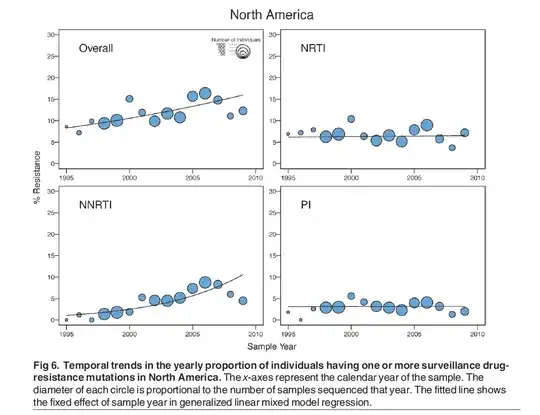
To draw the lines below, generalized linear mixed model regression is used in order to model the effect of time (represented on the x-axis) on percentage of TDR (represented on the y-axis). I would expect to see a linear increase over time, as it is linear regression. Why is it not the case?
Asked
Active
Viewed 207 times
1
-
2They have probably included a quadratic component, i.e. something like $\hat y=\beta_0 + \beta_1 x + \beta_2 x^2$ or perhaps some other non-linear transformation of the independent variable. – matteo Jan 22 '18 at 10:53
1 Answers
1
A generalized linear [mixed] model models a transformation of the expected value with a linear [mixed] model. The transformation is determined by a (potentially non-linear) link function, $g(x)$: $\mathbb{E}(Y)\sim g^{-1}(X\beta\, [+Zu])$.
Thus the inferred relationship is not necessarily linear.
See this question for an extended Explanation.
Furthermore, a linear model needs to be linear only in the coefficients, $\beta$, not the the independent variable. E.g. $y_i=\beta_0+\beta_1x_i+\beta_2x_i^2+e_i$ is linear in $(\beta_0, \beta_1, \beta_2)^T$.
jan-glx
- 341
- 1
- 9
-
Thanks. So no need to add a quadratic component as Matteo Lisi suggested? – Anthony Jan 22 '18 at 11:03
-
I noticed only now that the dependent variable is a probability, so they probably have used a non-linear link function, as indicated in @YAK answer (+1). In this case, you'd expect a non-linear relationship: the outcome is bounded in $(0,1)$ (0%- 100%) while the linear predictor (year) is not. – matteo Jan 22 '18 at 11:44