I have read that the variables must be approximately normally distributed to apply Pearson correlation; 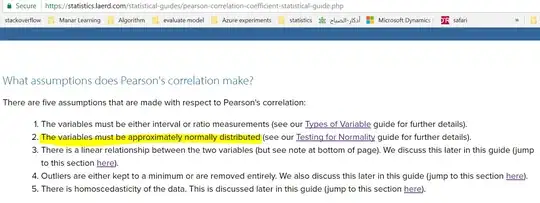
However, I came across this answer here that they dont need to be, so I am confused about that. Can i have a clarification about that ?
As Rob's answer in the post you link to would suggest, you certainly don't need it to calculate a Pearson correlation.
The need for normality would notionally apply if you used a test or interval that assumed normality in its calculations.
However, you can construct tests and intervals that avoid that assumption, if it's important to. For example, one could easily conduct a permutation test (a nonparametric test) of a Pearson correlation.
You should probably approach some of the advice you're getting at that site with some caution (e.g. see Harvey's answer at Is normality testing 'essentially useless'?)