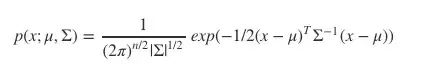0

The qualified question title hints at my not being certain as to what I'm really dealing with. I have some truly random samples that generate the following graph. This is just a small extract and many more readings can be had:-

log-normal?

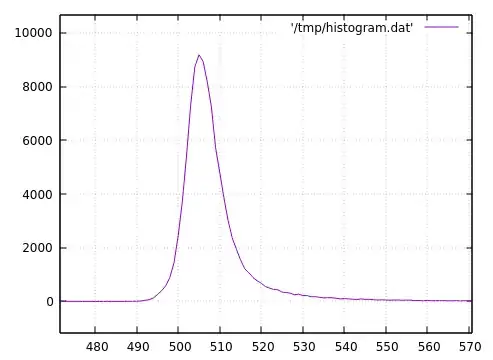
I've rotated the graph to the more typical orientation for a log normal distribution. The underlying theory behind the process suggests that they should be log normally distributed and it looks similar. However when I check Google Images for log normal, those graphs always seem to start exactly at zero. My data starts at ~490 units. This isn't my artificial offset, it's just how the sensor reads it.

So is this a log normal distribution, or is it something more exotic? And how would I fit a curve to it to obtain a mean and standard deviation please? I know how to transform to a normal distribution (by taking logs of the original data - example), but not if there's an offset.

This is the actual histogram of 100,000 samples:-

histogram

with the following descriptive statistics over the original samples:-

DescriptiveStatistics:
n: 100000
min: 480.0
max: 747.0
mean: 508.8298
std dev: 10.947259491986502
median: 507.0
skewness: 5.65519875015838
kurtosis: 58.297170613004134

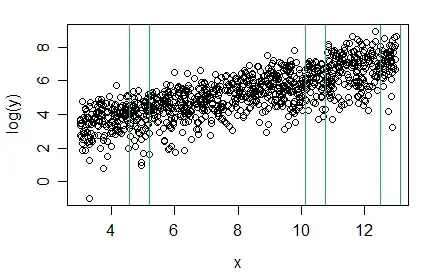
Since I was playing with Gnuplot, I then plotted a transform of log($1-479) which gave:-

log histogram

So I guess I've answered my own question. Still looks a bit skewy though. I guess it's now simply a matter of fitting a normal distribution to the transformed histogram...

kjetil b halvorsen
  • 63,378
  • 26
  • 142
  • 467
Paul Uszak
  • 494
  • 3
  • 17
  • 1
    Support of X (log-normally distributed random variable) is (0, + Inf). So it possible that your data possesses a log normal behaviour. Please try draw a histogram of your data and see the nature of histogram, it will definitely help you to decide underlying distribution. – Krishna Nevase Jan 04 '18 at 01:42
  • Can you not infer the histogram from the 500 data points on my graph? That's why I tilted it. It'll look exactly like a log normal but has the approximately 490 units offset. Values can go way above 640 if you wait long enough, but it'll never go down to 480 (in my life time). – Paul Uszak Jan 04 '18 at 01:57
  • yes, It is possible to draw a histogram for 500 data points. You can also look for goodness of fit tests. May be this question helps you- [How to determine which distribution fits my data best?](https://stats.stackexchange.com/questions/132652/how-to-determine-which-distribution-fits-my-data-best) – Krishna Nevase Jan 04 '18 at 03:17
  • 1
    @Paul you could draw a histogram (or something even more informative) much more easily than we can since you presumably have data. It's *very* hard to distinguish the distribution from the plot you have provided. Clearly the data cannot be an ordinary two-parameter lognormal, but it's possible that it's close to a shifted lognormal -- or perhaps any number of other options. – Glen_b Jan 04 '18 at 07:37

0 Answers0