Posterior Grid Approximation

Question

This might be a dumb question. I'm working on 2.11 in BDA (page 2 in this pdf http://www.uio.no/studier/emner/matnat/math/STK4021/h16/undervisningsmateriale/presentation_jariek.pdf). The problem is to find the posterior $\theta|y$ in the following model using a grid approximation: $$y|\theta\sim\textsf{Cauchy}(\theta,1),\ \theta\sim\textsf{Unif}(0,100).$$ On pages 3-4, it gives code for how to do this, along with how to sample from this approximate posterior (which I'll reproduce here, slightly altered):

dens <- function (y, th){
    dens0 <- NULL
    for (i in 1:length(th))
        dens0 <- c(dens0, prod (dcauchy (y, th[i], 1)))
    dens0
}
y <- c(43, 44, 45, 46, 46.5, 47.5)
step <- .01
theta <- seq(0, 100, step)
dens.unnorm <- dens(y,theta)
dens.norm <- dens.unnorm/(step*sum(dens.unnorm))
plot (theta, dens.norm, ylim=c(0,1.1*max(dens.norm)),
      type="l", xlab="theta", ylab="normalized density",
      xaxs="i", yaxs="i", cex=2, col="red", xlim=c(30,70))
thetas <- sample (theta, 1000, dens.unnorm, replace=TRUE)
hist(thetas, xlab="theta", yaxt="n", cex=2, add=TRUE, freq=F)

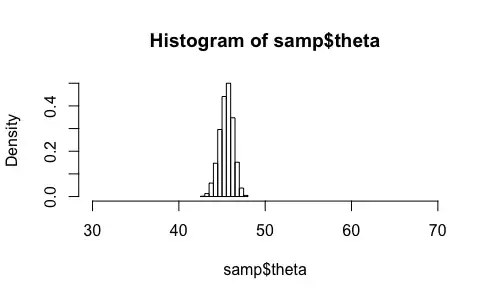
This produces the following plot, where the red curve is the approximate posterior and the histogram is comprised of 1000 samples from this approximate posterior:

What I don't understand is the line

dens.norm <- dens.unnorm/(step*sum(dens.unnorm))

where instead of just normalizing the sampled points by the sum of the sampled points, they multiply this sum by the step size of the grid (thus the density sums to 1/step instead of 1). In other sources I've found (for example McElreath's Statistical Rethinking pages 39-40), when doing a grid approximation they just normalize by the sum of the sampled points.

The resulting posterior approximation is definitely correct, as I've verified it in Stan:

data 
{
  int<lower=0> N;
  real y[N];
}
parameters 
{
  real theta;
}
model 
{
  theta ~ uniform(0, 100);
  y ~ cauchy(theta,1);
}

which produces these samples:

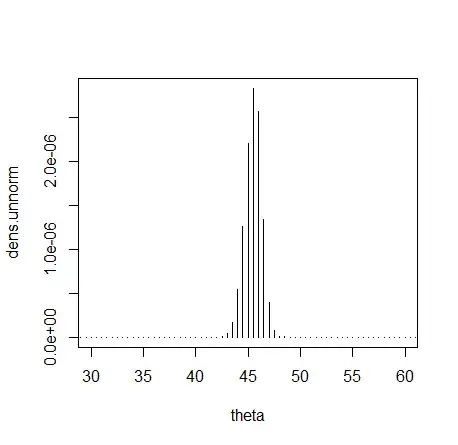
I've tried changing the line in question to

dens.norm <- dens.unnorm/(sum(dens.unnorm))

but this produces a density that's not properly normalized (even though it now sums to 1, it's the red that's barely visible at the bottom):

Anyone have any insight into what's going on here?

Answer 1

Change the step to something larger, e.g. step <- 0.5 and then plot it as a bar plot (i.e. plot(..., type = "h")), now look at the resulting plot.

The plot shows "samples" taken on a regular grid from the continuous density. The probability densities are unnormalized, to normalize them you would need to divide them by the total area under the curve, $\int f(x | \theta)\, \pi(\theta) \,d \theta$.

Look again at the above plot, do you have a curve and the area beneath it? No, you have just a set of points, so to calculate the area under the curve you are missing everything between the vertical bars. So instead $\int f(x | \theta) \,\pi(\theta) \,d \theta$, you do $\sum_{i \in G} f(x | \theta_i) \,\pi(\theta_i)$ where $G$ is just a small, finite subset of infinite number of the possible $\theta$'s. This is not the same.

If you had samples from this distribution and used histogram to estimate the empirical density, then you would split the samples in some number of boxes and then divide them by the sizes of the boxes and the total count, to get probability densities, i.e. "probabilities per foot". In the grid case you don't have samples scattered randomly, yet each of the "samples" represents a point in some neighborhood, so in fact you are approximating the continuous density with a "histogram", but with fixed points. So you are approximating the continuous curve with something looking more or less like the curve below.

To normalize the "histogram" you need to divide the "counts" by areas of the neighborhoods the points represent. Instead of dividing by the "masses" of the points, you divide by the areas of the rectangles they represent.