Why a T-statistic needs the data to follow a normal distribution

Question

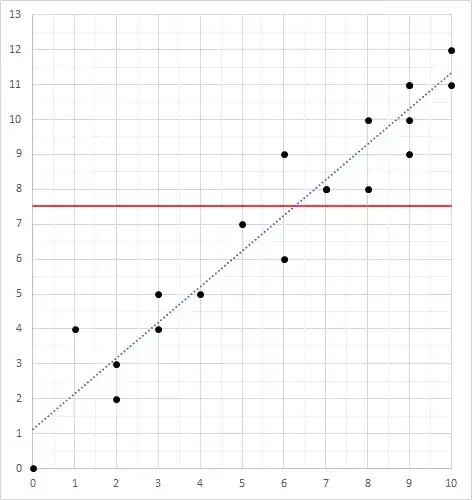
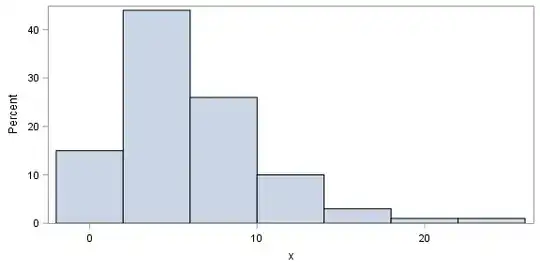
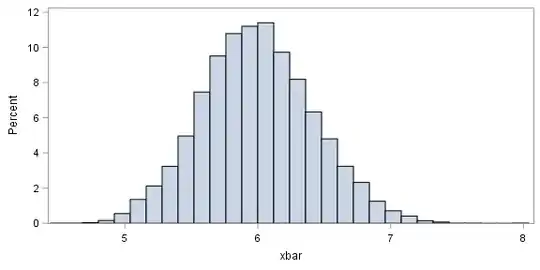
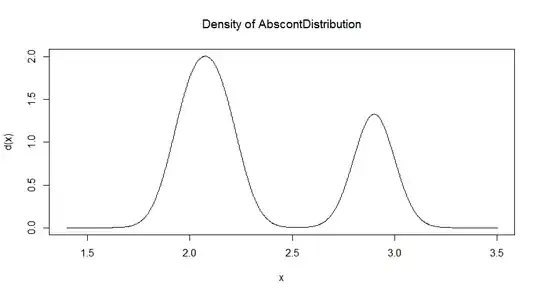
I was looking at this notebook, and I am puzzled by this statement:

When we talk about normality what we mean is that the data should look like a normal distribution. This is important because several statistic tests rely on this (e.g. t-statistics).

I don't understand why a T-statistic needs the data to follow a normal distribution.

Indeed, Wikipedia says the same thing:

Student's t-distribution (or simply the t-distribution) is any member of a family of continuous probability distributions that arises when estimating the mean of a normally distributed population

However, I don't understand why this assumption is necessary.

Nothing from its formula indicates to me that the data has to follow a normal distribution:

I looked a bit on its definition but I don't understand why the condition is necessary.

Answer 1

The information you require is in the "Characterization" section of the Wiki page. A $t$-distribution with degrees of freedom $\nu$ may be defined as the distribution of the random variable $T$ such that $$T = \dfrac{Z}{\sqrt{V/\nu}} \,,$$ where $Z$ is a standard normal distribution random variable and $V$ is a $\chi^2$ random variable with degrees of freedom $\nu$. In addition, $Z$ and $V$ must be independent. So given any $Z$ and $V$ that follow the above definition, you can then arrive at a random variable that has a $t$-distribution.

Now, suppose $X_1, X_2, \dots, X_n$ is distributed according to a distribution $F$. Let $F$ have mean $\mu$ and variance $\sigma^2$. Let $\bar{X}$ be the sample mean and $S^2$ be the sample variance. We will then look at the formulae:

$$\dfrac{\bar{X} - \mu}{S/\sqrt{n}} = \dfrac{\frac{\bar{X} - \mu}{\sigma/\sqrt{n}}}{\sqrt{\frac{(n-1)S^2}{(n-1)\sigma^2}}} \,.$$

If, $F$ denotes the normal distribution, then $\bar{X} \sim N(\mu, \sigma^2/n)$, and thus $\frac{\bar{X} - \mu}{\sigma/\sqrt{n}} \sim N(0,1)$. In addition, $\frac{(n-1)S^2}{\sigma^2} \sim \chi^2_{n-1}$ by Cochran's Theorem. Finally, by an application of Basu's theorem, $\bar{X}$ and $S^2$ are independent. This then implies that the resulting statistic has a $t$-distribution with $n-1$ degrees of freedom.

If the original data distribution $F$ was not normal, then, the exact distribution of the numerator and denominator will not be standard normal and $\chi^2$, respectively, and thus the resulting statistics will not have a $t$-distribution.

Answer 2

Just to add to the earlier responses something I think is relevant to the question, albeit possibly only indirectly: The normality of the data as pointed out in the answers is both necessary and sufficient for the t-statistic to have a t-distribution (hence, a characterization of it as a t-distributed random variable) because the normality of the data also characterizes the independence of the sample mean and sample variance (see, e.g., Lucaks (1942). A characterization of the normal distribution. Annals of Mathematical Statistics, 13(1), 91-93), which is crucial to the t-statistic having a t-distribution. An investigation of the necessity and sufficiency of the normality of the data for the t-distribution in this case is provided in Chen and Adatia (1997), "Independence and t distribution," The American Statistician, 51(2), 176-177.

Answer 3

I think there may be some confusion between the statistic and its formula, versus the distribution and its formula. You can apply the t-statistic formula to any dataset and get a "t-statistic", but this statistic will not be distributed according to the student-t distribution unless the data came from a normal distribution (or at least, will not be guaranteed to be; my guess is that non-normal distributions won't produce a student-t distribution when the t-statistic formula is applied, but I'm not certain of that). The reason for this is simply that the distribution of the t-statistic is calculated from the distribution of the data that generated it, so if you have a different underlying distribution, then you're not guaranteed to have the same distribution for derived statistics.

Answer 4

All that is needed is that $\bar{X}$ is normally distributed. If $\bar{X}$ is exactly normally distributed (not approximately normal) then the $X_i$ are normally distributed, $(n-1)S^2/\sigma^2$ is chi-square distributed and independent of $\bar{X}$, and $\frac{\sqrt{n}(\bar{X}-\mu)}{S}\sim T_{n-1}$. If $\bar{X}$ is only normally distributed asymptotically there is no guarantee that $\bar{X}$ and $S$ are independent nor that $(n-1)S^2/\sigma^2$ is chi-square distributed, but $\frac{\sqrt{n}(\bar{X}-\mu)}{S}\overset{asymp}{\sim}N(0,1)$ and of course a $T_{n-1}$ distribution and a $N(0,1)$ distribution are indistinguishable asymptotically.

Below is a histogram of $X_1,...,X_{100}\sim Gamma(2,3)$ with mean $\mu=2\times 3=6$, and below that is the sampling distribution of $\bar{X}$.

Of course the sample standard deviation is not independent of the sample mean as evidenced by the scatter plot below.

Nevertheless, the sampling distribution of $\sqrt{n}(\bar{X}-\mu)/S$ is well approximated by a $T_{n-1}$ distribution, i.e. $\sqrt{n}(\bar{X}-\mu)/S\overset{asymp}{\sim} T_{n-1}$.

For the distribution of $\sqrt{n}(\bar{X}-\mu)/S$ to be exactly $T_{n-1}$ distributed for any sample size then $X_i$ must come from a normal distribution.