Let’s say
$X_1$ ~ $uni(0,1)$
$X_2$ ~ $uni(0,1)$
$X_3$ ~ $uni(0,1)$
And
$Y=0.1X_1+0.3X_2+0.6X_3$
What’s the $F(Y)$ (i.e., CDF)?
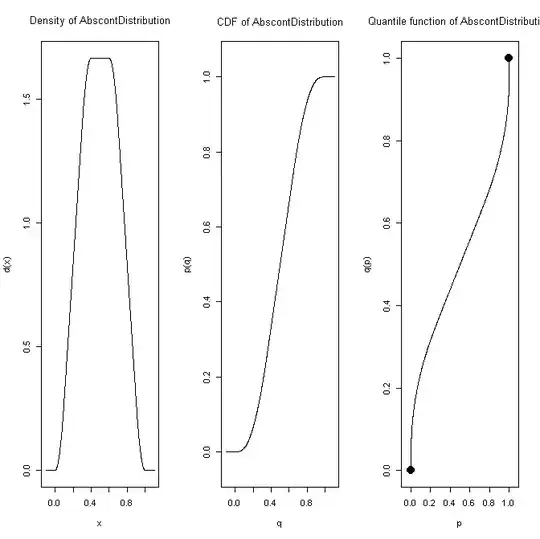
Let’s say
$X_1$ ~ $uni(0,1)$
$X_2$ ~ $uni(0,1)$
$X_3$ ~ $uni(0,1)$
And
$Y=0.1X_1+0.3X_2+0.6X_3$
What’s the $F(Y)$ (i.e., CDF)?
It is not one of the common named distributions, but the distr package in R can help you explore it:
library(distr)
d <- 0.1*Unif() + 0.3*Unif() + 0.6*Unif()
plot(d)