I have an experiment with three factors, say two machine vendors (factor: vendor) and each machine has two 'knobs' (factors: A, B) with each three levels. The measured output is continuous, and is measured independently 8 times for each combination of factors. The design is thus quite balanced, and there are 8*2*3*3=144 measurements.
The main questions is: Do both machines differ significantly in their output?
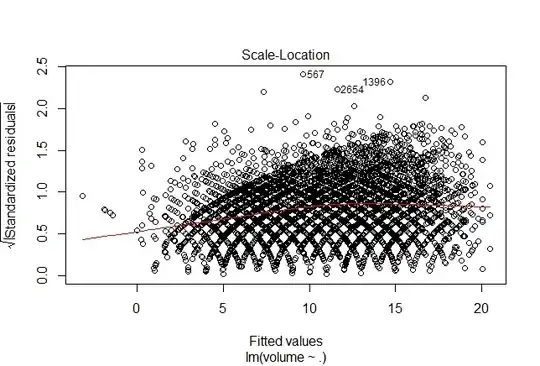
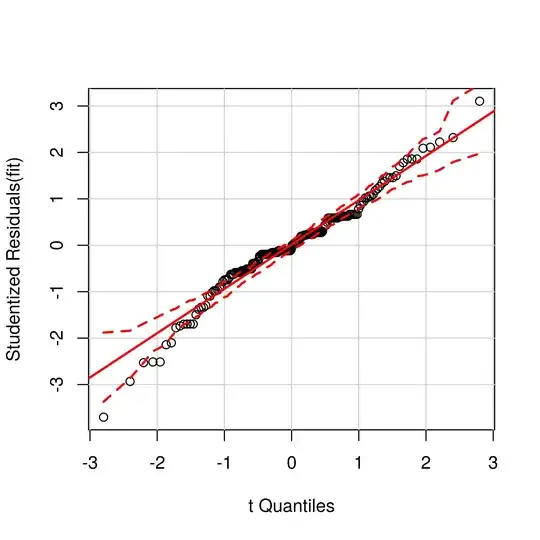
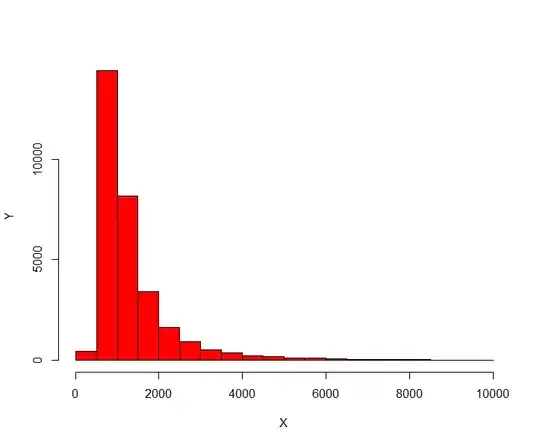
A three-way ANOVA would possibly work, but after fitting it, i have some non-normality in the residuals, tested with Shapiro-Wilk (with p<0.001). Also the groups are heteroscedastic, as the corresponding Levene test shows (also p<0.001).
I am confused what statistical model to use. Initially i thought a linear mixed model might be applied, but then both factors A,B only have 3 levels and probably most people would say that they should not be taken as random factors. I'd like to have a non-parametric ANOVA test, but which is the correct one? Personally i dislike the idea of transforming the outcome. Also i wonder if i should include all interactions or not.
Can anyone point me to the right test? Thanks!
Edit: As I use R, it would be great if I also could get a hint to the library to use.
Edit2: Here are some plots.