Somewhat loosely -- I have a coin in front of me. The value of the next toss of the coin (let's take {Head=1, Tail=0} say) is a random variable.
It has some probability of taking the value $1$ ($\frac12$ if the experiment is "fair").
But once I have tossed it and observed the outcome, it's an observation, and that observation doesn't vary, I know what it is.
Consider now I will toss the coin twice ($X_1, X_2$). Both of these are random variables and so is their sum (the total number of heads in two tosses). So is their average (the proportion of head in two tosses) and their difference, and so forth.
That is, functions of random variables are in turn random variables.
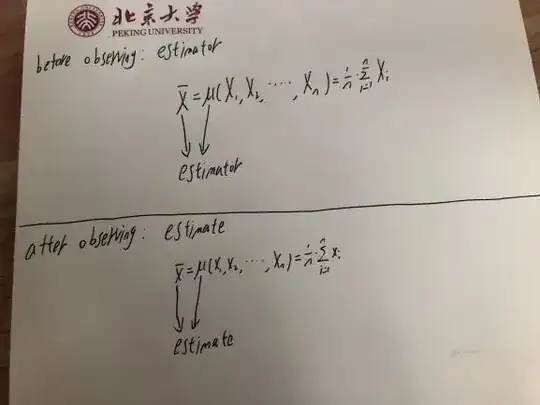
So an estimator -- which is a function of random variables -- is itself a random variable.
But once you observe that random variable -- like when you observe a coin toss or any other random variable -- the observed value is just a number. It doesn't vary -- you know what it is. So an estimate -- the value you have calculated based on a sample is an observation on a random variable (the estimator) rather than a random variable itself.