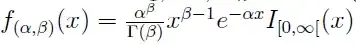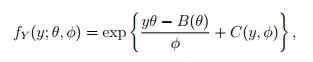As already recalled in the answer to a previous question of yours and well-explained on Wikipedia, for any exponential family, there exists a parameterisation such that the density of the family is$$f(x|\theta)=\exp\{\theta\cdot T(x)-\Psi(\theta)\}$$wrt a constant measure $\text{d}\mu(x)$, where the components of $T(\cdot)$ are linearly independent. The $\cdot$ in $\theta\cdot T(x)$ represents the scalar product, which means both $\theta$ and $T(x)$ are vector of the same dimension.
When you consider the density of the $\text{Ga}(\alpha,\beta)$ distribution,$$f(x|\alpha,\beta)=\dfrac{\beta^\alpha}{\Gamma(\alpha)}x^{\alpha-1}\exp\{-\beta x\}\mathbb{I}_{(0,\infty)}(x)$$moving terms into the exponential leads to
\begin{align*}
f(x|\alpha,\beta)&=\dfrac{\beta^\alpha}{\Gamma(\alpha)}x^{\alpha-1}\exp\{-\beta x\}\mathbb{I}_{(0,\infty)}(x)\\
&=\exp\{\log[\beta^\alpha] - \log \Gamma(\alpha)+[\alpha-1]\log x-\beta x\}\mathbb{I}_{(0,\infty)}(x)\\
&=\exp\{\underbrace{[\alpha-1]\log x-\beta x}_{\theta\cdot T(x)} + \underbrace{\log[\beta^\alpha] - \log \Gamma(\alpha)}_{\Psi(\theta)}\}\mathbb{I}_{(0,\infty)}(x)\\
\end{align*}
which suggests $\theta=(\alpha-1,\beta)$ as natural parameter and $T(x)=(\log x,-x)$ as sufficient statistic. (But other choices are possible.)
Hence, for this parameterisation of the $\text{Ga}(\alpha,\beta)$ distribution as an exponential family,
\begin{align*}
\Psi(\theta)&=-\log[\beta^\alpha] + \log \Gamma(\alpha)\\
&=-(\alpha-1+1)\log \beta + \log \Gamma(\alpha-1+1)\\
&= -[1+\theta_1]\log \theta_2 +\log \Gamma(1+\theta_1)
\end{align*}
as the cumulant moment function.