5

I have a histogram that looks like the following:

Histogram

From the data, I can see that this histogram shows two obvious curves. If I make the claim that they are from two Gaussians, how can I make a Gaussian mixture model to tell me the probabilities of an unseen x.

Is it possible to "learn" where the two Gaussian are in this histogram? After which, what is the accepted methodology for getting a probability from the GMM?

Nathan McCoy
  • 127
  • 1
  • 12
  • The EM algorithm does precisely what you want. Check out this [answer](https://stats.stackexchange.com/questions/268895/how-can-i-find-mean-and-covariance-after-em-iteration-on-gmm-algorithmm/270834#270834). – kedarps Nov 29 '17 at 18:31
  • Yes, but EM is usually for multidimensional inputs. My data is just a list of values which have this obvious gmm like shape after viewing them in a histogram. I'm having a hard time understanding how a list of values could be used in a GMM+EM framework. – Nathan McCoy Nov 29 '17 at 20:10
  • EM can be used for both univariate and multivariate data. In your case you have univariate data i.e. the Gaussians have support over R. For instance consider the code given [here](http://ogrisel.github.io/scikit-learn.org/sklearn-tutorial/modules/generated/sklearn.mixture.GMM.html) it uses univariate data. – kedarps Nov 29 '17 at 20:14
  • I will have to read more about EM to understand it thoroughly. I believe I have a misunderstanding about it fundamentally. I will also take a look at your links. It seems my question is reduced to: how do I model a GMM with univariate data? thank you @kedarps – Nathan McCoy Nov 30 '17 at 11:10
  • @kedarps if you make an answer with EM I will accept it. Thanks for your help. – Nathan McCoy Jan 19 '18 at 15:54
  • 1
    I think you don't have to restrict yourself to mixtures of Gaussians. There might be other distributions that work better with this data and a finite mixture approach. – dimitriy Jan 19 '18 at 19:30

1 Answers1

5

This example is demonstrated using Matlab. It can be easily adapted into Python or R.

Let's assume that your data contains a mixture of two underlying Gaussians, $\mathcal{N}(m_1, s_1)$ and $\mathcal{N}(m_2, s_2)$. Now, let's generate some sample data.

% define mean and variances of two Gaussians
m1 = -5; s1 = 4;
m2 = 2; s2 = 1;

% Generate some sample data
X = [m1 + s1*randn(1000, 1); m2 + s2*randn(1000, 1)];
% plot a histogram
hist(X, 250);

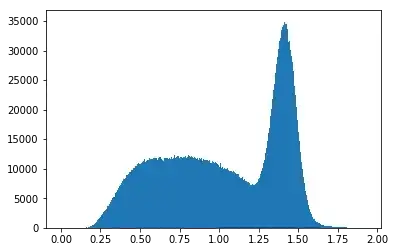
This is a histogram of the data generated, which looks quite similar to the data you have:

Histogram of generated data

Now given $X$, let's try to estimate the Gaussian mixtures. In Matlab (> 2014a), the function fitgmdist estimates the Gaussian components using the EM algorithm. 

% given X, fit a GMM with 2 components
gmm = fitgmdist(X, 2);

Here is a plot of the pdf of the estimated GMM, which very well matches the generated data:

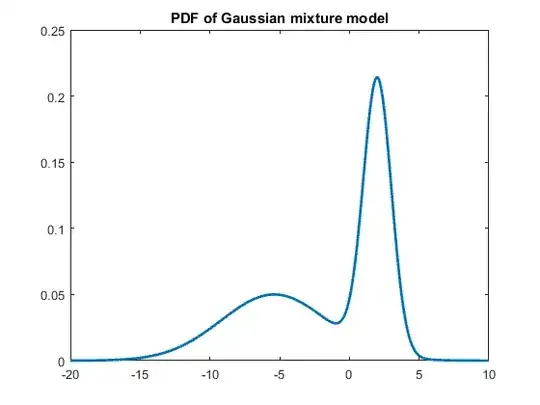
GMM distribution fit

Here are the Gaussian parameters estimated by the EM algorithm, which are pretty close to the true values that were used to generate the data:

% estimated parameters
m1_est = gmm.mu(1); % = 2.0086
m2_est = gmm.mu(2); % = -5.3910

s1_est = sqrt(gmm.Sigma(:,:,1)); % = 1.0134
s2_est = sqrt(gmm.Sigma(:,:,2)); % = 3.8199
  • For additional details on the EM algorithm, check this answer.
  • For a similar example using Python, see here.
kedarps
  • 2,902
  • 2
  • 19
  • 30