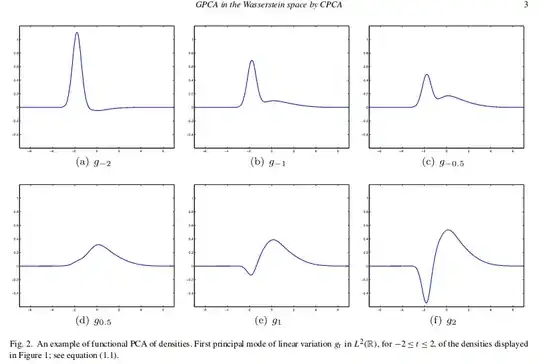
A proposal for this problem with probability measures can be found
Bigot et al. (2017). Geodesic PCA in the Wasserstein space by convex PCA. In Annales de l'Institut Henri Poincaré, Probabilités et Statistiques.
Given a set of curves $p_1 \ldots p_n \in L_2$ the first functional principal components can be formulated as the problem of finding a sequence of nested affine subspaces minimizing the sum of norms of projection residuals. In particular the first principal component is a solution of
$$ \min_{v \in L_2, \|v\| = 1} \sum_{i=1}^{n}d^2(p_i, S_v)$$
where $S_v = \{\bar p + tv, t \in \mathbb{R}\}$ and $d(x, S) = \inf_{x \in S} \| x - \bar p\|$.
Assuming $p_1. \ldots. p_n \in W_2$ the space of probability meassures with the Wasserstein metric, the proposed methodology in the paper is to change the distance defined by the euclidean metric to $d_W$ the Wasserstein metric. The first geodesic component is a solution of
$$ \min_{v \in W} \sum_{i=1}^{n}d_W^2(p_i, v).$$
The following figures copy pasted from the paper show the different results obtained for usual FPCA and GPCA. Since the minimizing of the second approach is done over $W$ the results obtained are probability measures.