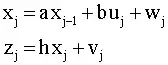You are talking about Bayesian analysis, not Bayes theorem, but we know what you mean.
Let me hit you with an idea that is even more strange than the one you are thinking about. As long as you use your real prior density in constructing your model, then all Bayesian statistics are admissible, where admissibility is defined as the least risky way to make an estimate. This means that even in the K-T example, you will get an admissible statistic. This does exclude the case of degenerate priors.
K-T do not directly discuss the formation of priors, but the idea you are trying to get across is the idea of predictive accuracy with flawed prior distributions.
Now let's look at Bayesian predictions under two different knowledge sets.
For purposes of exposition, it is to be assumed that the American Congress,
exercising its well-noted wisdom, and due to heavy lobbying by the Society of
American Magicians, has decided to produce magical quarters. They authorize
the production of fair, double-sided and biased coins. The double-headed
and double-tailed coins are easy to evaluate, but the two-sided coins are not
without flipping them.
A decision is made to flip a coin eight times. From those flips, a
gamble will be made on how many heads will appear in the next eight flips. Coins either have a 2/3rds bias for heads, a 2/3rds bias for tails, or it is a perfectly fair coin. The coin that will be tossed is randomly selected from a large urn containing a representative sample of coins from the U.S. Mint.
There are two gamblers. One has no prior knowledge, but the other phoned the US Mint to determine the distribution of the coins that are produced. The first gambler gives 1/3rd probabilities for each case, but the knowledgeable gambler sets a fifty percent probability on a fair coin, and even chances for either two from the remaining probability.
The referee tosses the coin, and six heads are shown. This is not equal to any possible parameter. The maximum likelihood estimator is .75 as is the minimum variance unbiased estimator. Although this is not a possible solution, it does not violate theory.
Now both Bayesian gamblers need to make predictions. For the ignorant gambler, the mass function for the next eight gambles is:
$$\Pr(k=K)=\begin{pmatrix}8\\ k\end{pmatrix}\left[.0427{\frac{1}{3}}^k{\frac{2}{3}}^{8-k}+.2737{\frac{1}{2}}^8+.6838{\frac{2}{3}}^k{\frac{1}{3}}^{8-k}\right].$$
For the knowledgeable gambler, the mass function for the next eight gambles is:
$$\Pr(k=K)=\begin{pmatrix}8\\ k\end{pmatrix}\left[.0335{\frac{1}{3}}^k{\frac{2}{3}}^{8-k}+.4298{\frac{1}{2}}^8+.5367{\frac{2}{3}}^k{\frac{1}{3}}^{8-k}\right].$$
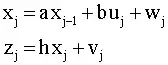
Even in this trivial case, the predictions do not match, yet both are admissible? Why?
Let's think about the two actors. They both have included all the information they have. There is nothing else. Further, although the knowledgeable actor does know the national distribution, they do not know the distribution to their local bank. It could be that they are all biased toward tails. Still, they both impounded all the information that they believe to be true.
Now let us again imagine that this game is played one more time. The two gamblers happen to be sitting side-by-side, and the ignorant gambler gets to see the odds of the knowledgeable gambler, and vice-versa. The ignorant gambler can recover the knowledgeable gambler's prior information at no cost by inverting their probabilities. Now both can use the extra knowledge.
The referee tosses four heads and four tails. This knowledge is combined to create a new prediction that is now joint among the gamblers. Its image is in the chart below.
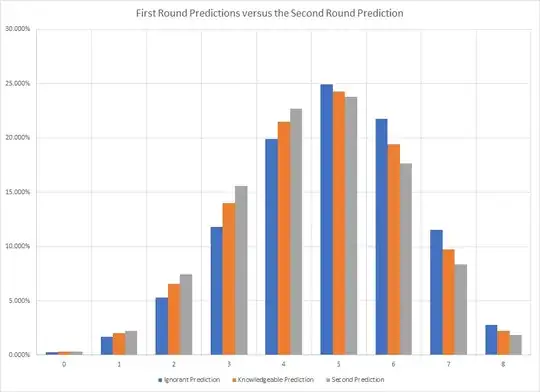
A gambler who had only seen four heads and four tails and had not seen the prior tosses may have yet a third prediction. Interestingly, for Frequentist purposes, you cannot carry information over to a second sample, so the prediction is independent of prior knowledge. This is bad. What if it has been eight heads instead, or eight tails. The maximum likelihood estimator and minimum variance unbiased estimator would be for a double-headed or double tailed coin with no variance either.
For this second round prediction, no admissible Frequentist estimator exists. In the presence of prior knowledge, Frequentist statistics cease being admissible. Now an intelligent statistician would just combine the samples, but that does violate the rules unless you are doing a meta-analysis.
Your meta-analysis solution will still be problematic, though. A Frequentist prediction could be constructed from the intervals and the errors, but it would still be centered on 10/16ths, which is not a possible solution. Although it is "unbiased" it is also impossible. Using the errors would improve the case, but this still is not equal to the Bayesian method.
Furthermore, this is not limited to this contrived problem. Imagine a case where the data is approximately normal, but without support for the negative real numbers. I have seen plenty of time series analysis with coefficients that are impossible. They are valid minimum variance unbiased estimators, but they are also impossible solutions as they are excluded by theory and rationality. A Bayesian estimator would have put zero mass on the disallowed region, but the Frequentist cannot.
You are correct in understanding that Bayesian predictions should be biased, and in fact, all estimators made with proper priors are guaranteed to be biased. Further, the bias will be different. Yet there is no less risky solution and when they exist, only equally risky solutions when using Frequentist methods.
The Frequentist predictions do not depend upon the true value of $p$, which is also true for the Bayesian, but does depend upon the count of observed outcomes. If the Frequentist case is included, the the prediction becomes the following graph.
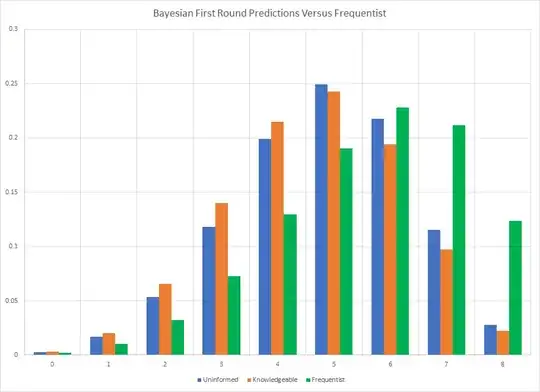
Because it cannot correct for the fact that some choices cannot happen, nor can it account for prior knowledge, the Frequentist prediction is actually more extreme because it averages over an infinite number of repetitions which have yet to happen. The predictive distribution turns out to be the hypergeometric distribution for the binomial.
Bias is the guaranteed price that you must pay for the generally increased Bayesian accuracy. You lose the guarantee against false positives. You lose unbiasedness. You gain valid gambling odds, which non-Bayesian methods cannot produce.