I am trying to build a multiple regression model while partitioning my data into subgroups based on additional set of covariates. While I implemented lmtree() or mob() in the "partykit" package, I tried to understand post-pruning strategies using AIC and BIC criterion, but I need some helps!
In the lmtree(), we can see the functions below:
"aic" = {
function(objfun, df, nobs) (nobs[1L] * log(objfun[1L]) + 2 * df[1L]) < (nobs[1L] * log(objfun[2L]) + 2 * df[2L])
}, "bic" = {
function(objfun, df, nobs) (nobs[1L] * log(objfun[1L]) + log(nobs[2L]) * df[1L]) < (nobs[1L] * log(objfun[2L]) + log(nobs[2L]) * df[2L])
}, "none" = {
NULL
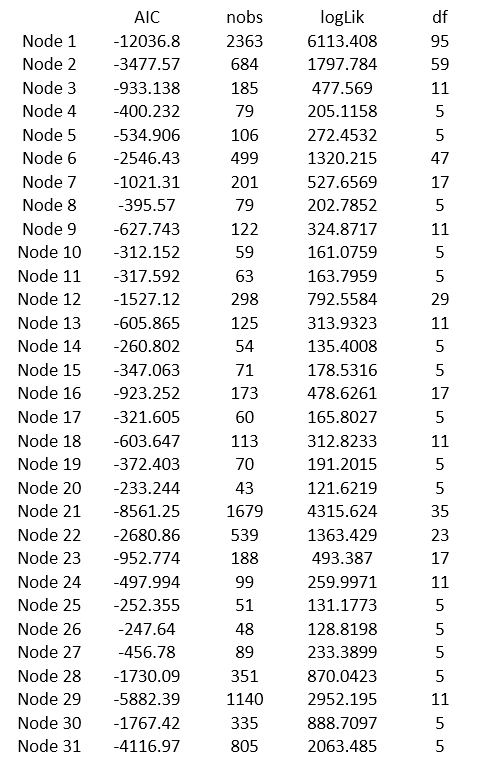
To understand how these functions cut some child nodes, I first grow a very large tree with control = mob_control(verbose=TRUE, ordinal = "L2", alpha=0.5) and save the results of AIC, nobs, logLik, and df values of each of the nodes (I saved these values to calculate the above AIC function manually):
Then, I fit another lmtree() function with mob_control(verbose=TRUE, ordinal = "L2", alpha=0.5, prune="AIC") to see which child nodes were cut. This results in a smaller tree without the nodes 4,5,8,9,10,11,14,15,19,20,24,25,26,27 from the first large tree.
I tried to calculate the AIC criterion value with the above table, e.g., starting from nodes 19 and 20, comparing node 18. However, as I kept pruning the tree from the bottom, it seems that the calculation in lmtree() are not always correct... Can you clearly explain what are the objfun[2], nobs[2], and df[2] in the AIC and BIC functions? For example, after I cut the nodes 10 and 11, how I can decide to keep the nodes 8 and 9 comparing with node 7?
Thank you so much for your time in advance!