The one-way random effects model for balanced data as described by Swamy/Arora (1978) is extended to the unbalanced case in Baltagi/Chang (1994) (another exposition is in Baltagi's text book). Various software packages claim to implement it. However, I found a little difference between some software packages for the associated standard errors (but coefficients match) and also the original Baltagi/Chang (1994) paper. I am looking for an explanation why the standard errors diverge a little bit.
The difference becomes visible with heavily unbalanced data sets, I am taking the hedonic house pricing data (Harrison/Rubinfeld (1978)) as an example as it also serves as the empirical example in the original paper.
Results of EViews agree with the original paper, but diverge from results of R's plm (1.6-6) package and from gretl (2017d with Baltagi/Chang option selected) while the latter two match each other's values. (Be sure to use these latest versions of the respective software, if you care to perform the estimation yourself.)
Here is example code for R:
# scaling of variables in dataset Hedonic is a little bit different to Baltagi/Chang (1994) and Baltagi's text book, table 9.1
# see below for scaling as in Baltagi/Chang (1994)
library(plm)
data("Hedonic", package = "plm")
pHedonic <- pdata.frame(Hedonic, index = "townid")
form <- formula(mv ~ crim + zn + indus + chas + nox + rm + age + dis + rad + tax + ptratio + blacks + lstat)
## do (weired) scaling of variables as in Baltagi/Chang (1994)
Hedonic$mv2 <- Hedonic$mv
Hedonic$crim2 <- Hedonic$crim / 100
Hedonic$zn2 <- Hedonic$zn / 1000
Hedonic$indus2 <- Hedonic$indus / 100
Hedonic$chas2 <- (as.numeric(Hedonic$chas)-1) / 10
Hedonic$nox2 <- Hedonic$nox / 100
Hedonic$rm2 <- Hedonic$rm / 100
Hedonic$age2 <- Hedonic$age / 1000
Hedonic$dis2 <- Hedonic$dis / 10
Hedonic$rad2 <- Hedonic$rad / 10
Hedonic$tax2 <- Hedonic$tax / 1000
Hedonic$ptratio2 <- Hedonic$ptratio / 100
Hedonic$lstat2 <- Hedonic$lstat / 10
pHedonic2 <- pdata.frame(Hedonic, index = "townid")
form2 <- formula(mv2 ~ crim2 + zn2 + indus2 + chas2 + nox2 + rm2 + age2 + dis2 + rad2 + tax2 + ptratio2 + blacks + lstat2)
summary(plm(form2, data = pHedonic2, model = "random"))
## Coefficients:
## Estimate Std. Error t-value Pr(>|t|)
## (Intercept) 9.685867 0.197510 49.0398 < 2.2e-16 ***
## crim2 -0.741197 0.104781 -7.0738 5.211e-12 ***
## zn2 0.078877 0.650012 0.1213 0.9034662
## indus2 0.155634 0.403491 0.3857 0.6998718
## chas2 -0.044247 0.292118 -0.1515 0.8796662
## nox2 -0.584251 0.124518 -4.6921 3.510e-06 ***
## rm2 0.905517 0.118863 7.6182 1.331e-13 ***
## age2 -0.857873 0.467933 -1.8333 0.0673581 .
## dis2 -1.444184 0.440937 -3.2753 0.0011301 **
## rad2 0.959839 0.266109 3.6069 0.0003415 ***
## tax2 -0.377396 0.176926 -2.1331 0.0334132 *
## ptratio2 -2.947578 0.906984 -3.2499 0.0012336 **
## blacks 0.562775 0.101974 5.5188 5.529e-08 ***
## lstat2 -2.910749 0.239273 -12.1650 < 2.2e-16 ***
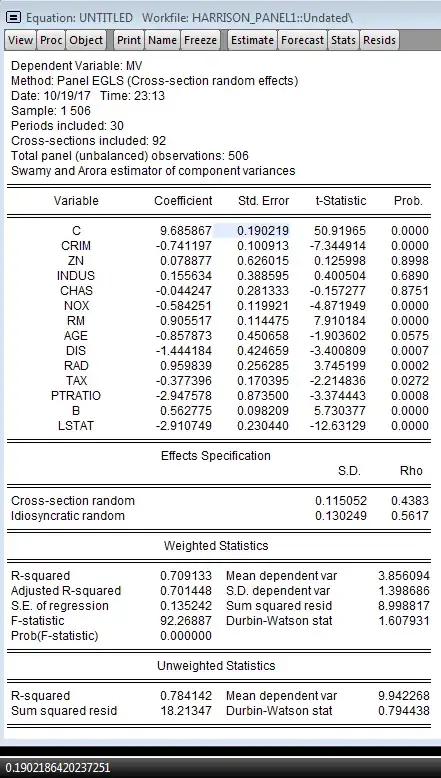
Here is EViews' output for the same model:
Note how the coefficients match exactly, but the standard errors diverge, e.g. for the intercept plm (and gretl) estimates the standard error to be 0.197510 and while EViews gives 0.190219. The different standard errors are proportionate by about 0.9631.
All three implementations claim to use the "ordinary" way (like in OLS) to estimate the standard errors (covariance matrix: s^2 * (Z'Z)^(-1) where Z is the quasi-demeaned data) and I can confirm so for plm and gretl (open source). The "standard error of regression"/sigma matches (0.1352416). All estimations have been carried out without any option for robust standard errors. I would blame closed-sourced EViews to do something "wrong", but they match the original paper's values for the standard errors (presented there by two decimals only) - which is even more interesting. So - as it seems equivalantly - my question can also be answered by showing what Baltagi/Chang did in their original paper.
I do not think it is a rounding issue as the coeffiecients match up to machine precision.
EDIT: There is some more information in the EViews forum about this (see http://forums.eviews.com/viewtopic.php?f=4&t=18629).
(Side note: Stata does something different, even for the Swamy/Arora option, and I know what it does. While this is an interesting point as well, it shall be left out of this question's scope.)