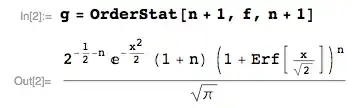Question:
Let:
- $(X_1, X_2, \dots, X_n, X_{n+1})$ denote a sample of size $(n+1)$ on random variable $X$ with pdf $f(x)$
- $M_n$ denote the maximum of the first $n$ values, and $M_{n+1}$ the sample max of all $n+1$ values
- $g(x_{(n+1)})$ denote the pdf of the sample maximum, given a sample of size $n+1$.
- $g(x_{(n)},x_{(n+1)})$ denote the joint pdf of the $n^{\text{th}}$ and $(n+1)^{\text{th}}$ order statistics in a sample of size $n+1$ (i.e. the joint pdf of the second largest and largest values).
The pdf of $g$ and pdf of $g(.,.)$ are textbook material, and can be expressed as a function of $f(x)$.
The question is to find the joint pdf of $(M_n, M_{n+1})$.
Answer:
There are two possibilities:
1) $X_{n+1} \leq M_n$, in which case $M_{n+1}= M_n$. This happens with probability $\frac{n}{n+1}$.
or
2) $X_{n+1} > M_n$, in which case $M_{n+1} > M_n$. This happens with probability $\frac{1}{n+1}$.
Accordingly, the joint pdf of $(M_n, M_{n+1})$ can be written:
$$\text{pdf}(M_n, M_{n+1}) = \left\{
\begin{array}{cc}
\frac{n}{n+1} g(x_{(n+1)}) \;\;\;\; & \text{if } M_{n+1} = M_{n}\\
\frac{1}{n+1} g(x_{(n)}, x_{(n+1)}) & \text{if } M_{n+1} > M_{n} \\
\end{array}
\right. $$
Example (with simulation check)
Let the parent random variable $X$ be standard Normal with pdf $f(x)$:

Then, the pdf of the sample maximum, in a sample of size $n+1$, is $g(x_{(n+1)})$:
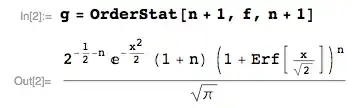
where I am using the OrderStat function from the mathStatica package for Mathematica to automate,
and the joint pdf of the $n^{\text{th}}$ and $(n+1)^{\text{th}}$ order statistics in a sample of size $n+1$ is $g(x_{(n)}, x_{(n+1)})$:

Simulation check
The following Monte Carlo check generates 10 million samples, each of size $n = 10$. For each case, it then generates an $11^\text{th}$ term, and compares it to the first 10 values.
- In $\frac{10}{11}$ cases, the $11^\text{th}$ term will be smaller than $M_{10}$, in which case $M_{11} = M_{10}$. The following diagram compares the empirical pdf of $M_{11}$ (blue) to the theoretical solution $g(x_{(11)})$ derived above (red dashed). They are so close, it is difficult to see any difference.
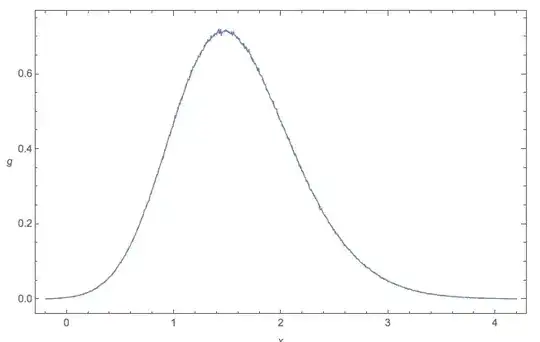
- In $\frac{1}{11}$ cases, the $11^\text{th}$ term will be LARGER than $M_{10}$, in which case $M_{11} > M_{10}$.
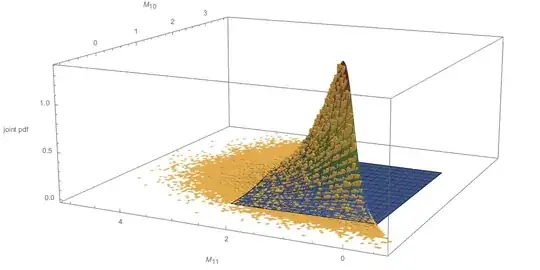
The following diagram plots the exact theoretical solution $g(x_{(10)}, x_{(11)})$ derived above:
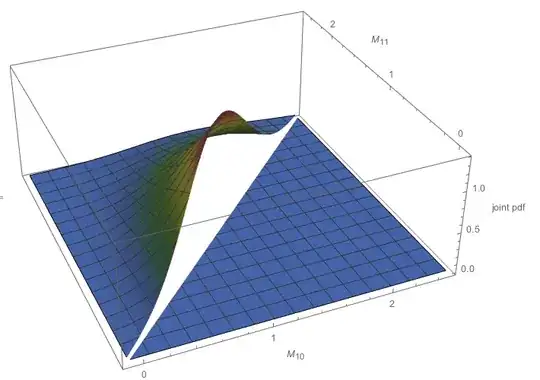
Finally, the next diagram compares the empirical joint pdf of $(M_{10}, M_{11})$ to the theoretical solution $g(x_{(10)}, x_{(11)})$ derived above: