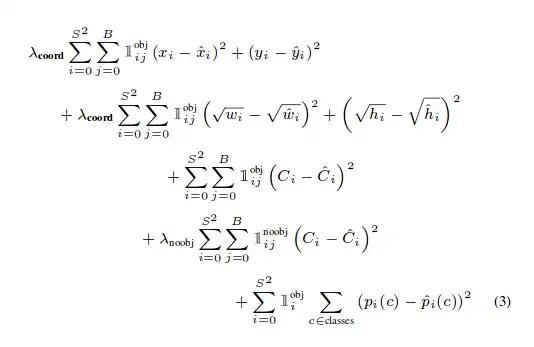4

I'm trying to work on a Yolo implementation which searches a 19x19 grid to find a specific item. There is only a single class in all of these images I am looking to get bounding boxes for. I'm a little confused about the calculation of the loss function though.

Calculation of loss function from the Yolo paper

The output from my CNN is a 19x19x5 matrix (P , x , y , w , h), with P being the probability that an object is located in this frame.

The way I've interpreted this function is as follows: - Add the sum of squares of the x and y coordinates from true and pred - Multiply by 1 if the ground truth object is present, otherwise 0 - Multiply by 5 to increase the loss from bounding boxes

-repeat this with the sum of squares of the square root of w and h

Here is the part that confuses me now. Since I do not have any classes, only a probability of object being in this frame, I'm not sure how to account for this.

Should I treat C as equal to P, and simply take the sum of squares as: 1obj (Pi - Ptruei) + 0.5* 1noobj (Pi-Ptruei)

My guess is that if the object is located in that cell, this loss function would penalize localization error to a greater extent. Whereas if there are no objects, it will penalize the probability of the object.

Stephan Kolassa
  • 95,027
  • 13
  • 197
  • 357
Michael Bawol
  • 151
  • 4

1 Answers1

1

I think you just can exclude the last term from loss function if you only have one class. This should make sense since the last term is responsible for training the net to classify objects in a cell. If there are no classes there is nothing to classify. And C in this formula denotes the confidence, which is simply IoU(truth, predicted).

Andrew
  • 121
  • 1