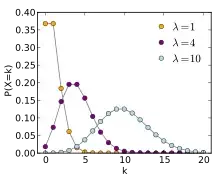
The above image shows a Poisson distribution for different values of the mean $\lambda$. If I was to fix a value of $k$ (say $k=3$) and sum over the different $\lambda$, is it true that $\sum_{\lambda}P(X=k| \lambda) = 1$?
If not, is there an obvious way to adapt this distribution so that this property is satisfied?