0

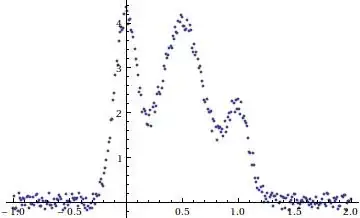
In the plot we see a mean zero process. It not entirely normally distributed. How can I find a suitable distribution for this process? It needs to be white noise and hence iid. enter image description here enter image description here

Kareshma
  • 1
  • 1
    "Normally distributed" is not a [requirement of white noise.](https://en.wikipedia.org/wiki/White_noise#Mathematical_definitions). What is your actual problem then? – whuber Nov 03 '17 at 21:14
  • "suitable" for what purpose? How much will deviations matter, and of what kind? Do you actually need an explicit functional form, or is the purpose one for which an explicitly-written density is not necessary? – Glen_b Nov 04 '17 at 01:37

1 Answers1

1

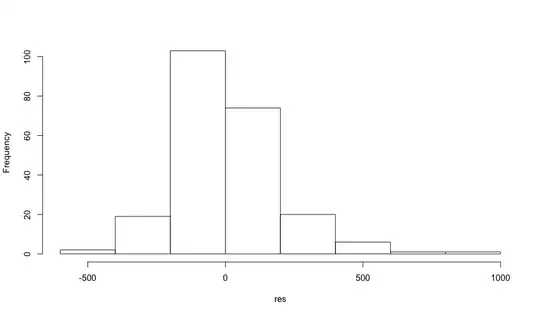
The shape of your histogram appears to be potentially Log-Normal with a negative shift. I would shift all of these values positively by $|min(x) + \epsilon|$ so that your support is non-negative, then overlay a log-normal density to see if it matches (where $\epsilon$ is some arbitrarily small number).

Here's a histogram of some random lognormal data that I shifted by $-1000$. It's probably close enough to what you need show my point that you should shift your observations into the positives and try to fit a distribution after that.

histogram

This is a an exponentiated random normal distribution with mean 1 and standard deviation 0.20 premultiplied by 400. Here's the R code I used: x <- 400 * exp(rnorm(1000, mean = 1, sd = 0.20)) hist(x - 1000)

Gabriel J. Odom
  • 300
  • 1
  • 7
  • Consider asking the OP for clarification: these are likely residuals, for which no such shift would be feasible. Even if not, adding the minimum won't work, because you cannot take the log of zero. See, for instance, https://stats.stackexchange.com/questions/30728 or https://stats.stackexchange.com/questions/298. The departure from normality is so mild it seems worthwhile questioning why this question is even being asked--the details might mask a more important question for which taking logs might not be the answer. BTW, welcome to our site! – whuber Nov 03 '17 at 21:46
  • 1
    @whuber: Thank you for your comment and warm welcome. Due to my low reputation, I was prohibited from asking for clarification in a comment. Beginners are stuck writing answers to questions posed by other beginners, so it's a rather ugly situation for folks with low reputation. I did edit my comment to address the minimum / log(0) concern. – Gabriel J. Odom Nov 07 '17 at 16:37