2

I have trained a model of Ridge classifier on the following dataset:

X = [[2,1], [2,3], [1,2], [3,2], [5,2], [5,4], [6,3]]

y = [1, 1, 1, 1, 0, 0, 0]

In the second example i add a new example [12,8] to X and train. Why does regression behave in such way that it readjusts the boundary, kicking the example (5,4) on the other side ?

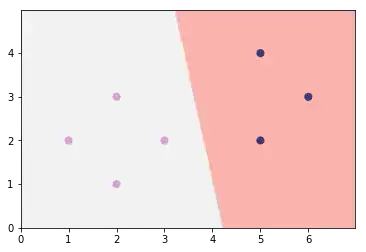
linear_regression_1 linera_regression_2

whuber
  • 281,159
  • 54
  • 637
  • 1,101
monolith
  • 123
  • 6

2 Answers2

1

New, corrected answer: (just putting bibliolytic's answer into pictures)

Let us take a one dimensional situation. We have one input feature $x$ from which we want to predict some boolean valued $z$. The first thing we do is cast $z$ to a real value like so: false becomes $-1$ and true becomes $1$. Then we compute a usual regression model $L$ and make the prediction as follows: $x$ gets predicted as true iff. $L(x) > 0$. Let us assume that we have the following data set:

 x |  y
-1 | -1
 0 | -1
+1 | +1

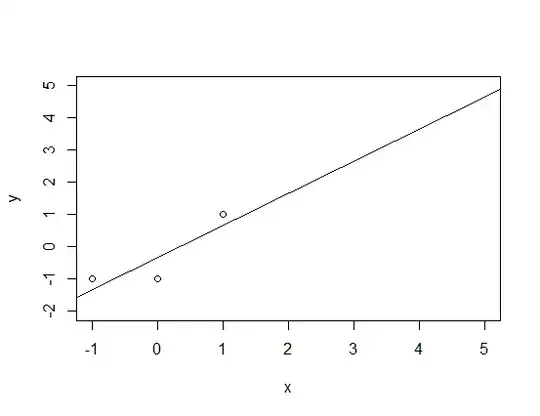
we learn the model $L(x) = x - 1/3$: enter image description here

Now let us see what happens when we insert a new point far away (say a positive sample for $x=5$) into the image: 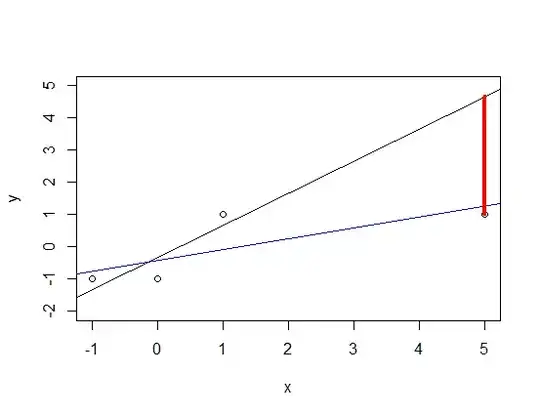enter image description here The old regression line (black line) does not fit the data anymore but the interesting thing is why it does so: By doing a linear regression and ignoring the fact that $y$ is actually $-1, +1$--valued one punishes 'the red line'! Although we have a predictor that says 'if $L$ is big then I predict true' and the value of $L$ is very big at $x=5$ one still punishes the model. One should not do that because the old black line would suit the situation just fine!

The new regression line must adapt to this large red gap: As it is the line that produces the least error (and it has the highest possibility of making an error at $x=5$) it will fit $x=5$ particularly well but then it has to 'bow down' around the origin causing the line to predict $L(0) \approx -0.08$, i.e. our prediction at $x=1$ would become false; the model 'kicks' out this positive sample from the positive region!

Old, wrong answer:

Basic answer: This happens because you are using a regularization. In general you want your model to represent the data as good as possible. This means that you normally introduce some kind of error function $l$ (for a classification as you did above that is called 'logistic regression' it is usually the cross entropy loss) and minimize the function $$L(\text{model}) = \sum_{i=1}^n l(\text{model}(x_i), y_i)$$ i.e. you minimize how far the model answer was away from the real answer. Here, $x_1, ..., x_n$ are the inputs and $y_1, ..., y_n$ are the observed/desired outputs. However, you can always find a model that has 'zero error': Just make a final case distincting giving $y_i$ if the input was exactly $x_i$ and some other random value otherwise. This model is obviously shitty, hence one only allows for special models (for example, one introduces the restriction 'the model must be of a linear form'). Then one realizes that still, the model may overfit the data (i.e. it makes the coefficients unusually big just to include one single positive outlier that actually should not be a positive sample). One wants to exclude these models as well, hence one wants to put a restriction on the model like 'do not make the coefficients too big'. This is done by adding a so-called regularization term $\Omega(\text{model})$ and now one minimizes $$L(\text{model}) + \Omega(\text{model})$$ i.e. the regression line that you got out has the minimal 'composed error' (=error on the training set plus regularization). For example: If you make the regularization (coefficients) unusually high then the model will not care at all about whether or not it does something senseful on the training data because the dominating term will be $\Omega(\text{model})$. So it might happen that the model does not classify only a single instance correctly but is the 'best possible model' when minimizing the composed function

Fabian Werner
  • 3,055
  • 1
  • 9
  • 25
  • Or rather: If you want the model to *not* kick the sample out of the right half space then make the regularization coefficient(s) smaller or remove it completely and traing a pure logistic regression without regularization (might work if you put the regularization to zero, possibly depends on the implementation) – Fabian Werner Nov 03 '17 at 14:11
  • I get what you are trying to say, but i trained the classifier with alpha parameter set to 0, meaning there is no regularization. I also trained a simple linear regression with hypothesis f = lambda x: lr.predict(x) >= 0.5 and got the same results. So i think this isn't much to do with regularization. – monolith Nov 03 '17 at 14:13
  • The distance of example from the boundary is given by $\frac{h(x)}{||w||}$ meaning the further the example is from the boundary the bigger h(x) and we need bigger weights to adjust. In consequence the boundary is tilted and (5,4) falls out because it's h(x) is not enough to classify it as the "right-class" - This was my first guess. – monolith Nov 03 '17 at 14:22
  • Humm... if you set the regularization to zero then in theory (your data is separable) the linear separation line must separate the data. Hence, it must have something to do with the optimization internals... In the end: We must minimize a complicated function using some strategy like gradient descent... – Fabian Werner Nov 03 '17 at 14:27
  • Using ordinary least squares closed-form solution yields same results... – monolith Nov 03 '17 at 14:30
  • Sorry, I keep on forgetting that: Perfect separation seems to be a problem for logistic regression so (as far as I understood) you must use some kind of regularization (even though you set it to zero manually)... see https://stats.stackexchange.com/questions/11109/how-to-deal-with-perfect-separation-in-logistic-regression – Fabian Werner Nov 03 '17 at 14:31
  • So @FabianWerner thats really not true...he's not using a margin-based classifier. Linear regression used for classification has no requirement whatsoever to perfectly separate your classes – bibliolytic Nov 03 '17 at 14:31
  • What do you people actually mean when you say 'linear regression for classification'? You need to setup some likelihood or log loss function that you maximize or minimize... what should that be for classification? Do you interpret y=true as 1 and y=false as 0 and do a usual regression? – Fabian Werner Nov 03 '17 at 14:32
  • that would be logistic--see my answer below for the linear regression-classification thing. – bibliolytic Nov 03 '17 at 14:34
  • $ h(x) = $ True if $w^{T}x+w_0 > 0.5 $ else false for {0,1} binary classification – monolith Nov 03 '17 at 14:34
  • @wedran that is the prediction (I understand that) but how do you measure how far the prediction is from the actual observed value? You need to minimize this quantity... – Fabian Werner Nov 03 '17 at 14:36
  • @wedran why > 0.5? Geographically speaking, this just moves the line and could be packed into the $w_0$ as well. Furthermore, the $w^Tx + w_0$ does not produce values in $[0,1]$ but general numbers in $\mathbb{R}$ – Fabian Werner Nov 03 '17 at 14:38
  • @FabianWerner The closed-form solution of OLS is implicitly given by maximizing likelihood, or minimizing negative log-likelihood – monolith Nov 03 '17 at 14:39
  • Yes, but what is the likelihood? Respectively: what is the error function that needs to be minimized? $y_i - \text{model}(x_i)$? That hardly makes sense because $y_i$ is a true/false variable... you somehow need to interpret this as 0/1 and even then its not a good idea to do something simple as this because then the model gets penalized independently of how far it is off the track so it does not know in which direction to got in order to get any better! – Fabian Werner Nov 03 '17 at 14:41
  • @FabianWerner Using Linear regression i get real number values for output. When the examples are clustered as in example 1) i get perfect {0,1} prediction. But when one example deviates as in example 2) i get output values like [0.67600701 0.98423818 1.03152364 0.62872154 0.22591944 0.53415061 0.17863398 -0.2591944 ]. Now i realize- that might be the problem. That i use a 0.5 as margin for classification, because all this examples are assumed to be perfectly clustered – monolith Nov 03 '17 at 14:50
  • Ah only now I understand what you are actually doing: you cast the true/false column as 0/1 and then you do a usual regression as if y was just some numeric vector... then you punish the distance from the regression plane (must go towards infinity for points far away) from something that can only be 0/1... no wonder there are fishy things happening at the boundary. @bibliolytic: You were absolutely right, my bad. I'll remove my answer asap!! – Fabian Werner Nov 03 '17 at 15:16
  • @wedran: I have adapted the answer to the one of bibliolytic. – Fabian Werner Nov 10 '17 at 16:38
  • Thank you, and if i I may add ti your answer. The original problem was using the MSE as the error function, because it penalizes even the correctly classified examples. For example using logistic regression doesn't behave in the same way. As you said, the model rather kicks out the example (-1,1) because it's h(x) is so little (which relates to the distance to the hypothesis), and it has less influence to the total error in favor of minimizing the red distance in your example. – monolith Nov 11 '17 at 14:46
0

It's not regularization, it seems to me. A ridge classifier does linear regression to find the line that best fits your points, then to do the classification part it essentially projects your new points onto this line and looks whether the new point is closer to 0 or 1.

The issue is that, since you have very few points and your final point is far from the other ones, you're skewing the initial linear regression step quite strongly. I don't know the stackoverflow editing commands well enough to show this myself, but it should be visible if you plot the straight linear regression solution given those x's and y's.

bibliolytic
  • 589
  • 3
  • 10
  • As i already stated in the comment below, i did not use any regularization and i got the same results using a simple Linear regression http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html – monolith Nov 03 '17 at 14:25
  • Right, which suggests that my second paragraph solves your problem. Your last point is an outlier and linear regression is very susceptible to outliers – bibliolytic Nov 03 '17 at 14:30
  • Yes, i am aware, but i am intersted in specific math behind it... – monolith Nov 03 '17 at 14:32
  • have you computed the OLS solutions by hand/machine? – bibliolytic Nov 03 '17 at 14:36
  • Using sklearn.linear_model module in python like so rc = RidgeClassifier(alpha=0, solver='lsqr') – monolith Nov 03 '17 at 14:43