Consistency is obviously a natural and important property of estimators, but are there situations where it may be better to use an inconsistent estimator rather than a consistent one?
More specifically, are there examples of an inconsistent estimator which outperforms a reasonable consistent estimator for all finite $n$ (with respect to some suitable loss function)?
This answer describes a realistic problem where a natural consistent estimator is dominated (outperformed for all possible parameter values for all sample sizes) by an inconsistent estimator. It is motivated by the idea that consistency is best suited for quadratic losses, so using a loss departing strongly from that (such as an asymmetric loss) should render consistency almost useless in evaluating the performance of estimators.
Suppose your client wishes to estimate the mean of a variable (assumed to have a symmetric distribution) from an iid sample $(x_1, \ldots, x_n)$, but they are averse to either (a) underestimating it or (b) grossly overestimating it.
To see how this might work out, let us adopt a simple loss function, understanding that in practice the loss might differ from this one quantitatively (but not qualitatively). Choose units of measurement so that $1$ is the largest tolerable overestimate and set the loss of an estimate $t$ when the true mean is $\mu$ to equal $0$ whenever $\mu \le t\le \mu+1$ and equal to $1$ otherwise.
The calculations are particularly simple for a Normal family of distributions with mean $\mu$ and variance $\sigma^2 \gt 0$, for then the sample mean $\bar{x}=\frac{1}{n}\sum_i x_i$ has a Normal$(\mu, \sigma^2/n)$ distribution. The sample mean is a consistent estimator of $\mu$, as is well known (and obvious). Writing $\Phi$ for the standard normal CDF, the expected loss of the sample mean equals $1/2 + \Phi(-\sqrt{n}/\sigma)$: $1/2$ comes from the 50% chance that the sample mean will underestimate the true mean and $\Phi(-\sqrt{n}/\sigma)$ comes from the chance of overestimating the true mean by more than $1$.
The expected loss of $\bar{x}$ equals the blue area under this standard normal PDF. The red area gives the expected loss of the alternative estimator, below. They differ by replacing the solid blue area between $-\sqrt{n}/(2\sigma)$ and $0$ by the smaller solid red area between $\sqrt{n}/(2\sigma)$ and $\sqrt{n}/\sigma$. That difference grows as $n$ increases.
An alternative estimator given by $\bar{x}+1/2$ has an expected loss of $2\Phi(-\sqrt{n}/(2\sigma))$. The symmetry and unimodality of normal distributions imply its expected loss is always better than that of the sample mean. (This makes the sample mean inadmissible for this loss.) Indeed, the expected loss of the sample mean has a lower limit of $1/2$ whereas that of the alternative converges to $0$ as $n$ grows. However, the alternative clearly is inconsistent: as $n$ grows, it converges in probability to $\mu+1/2 \ne \mu$.
Blue dots show loss for $\bar{x}$ and red dots show loss for $\bar{x}+1/2$ as a function of sample size $n$.
Here is a very real situation where an inconsistent estimators is preferable due to constraints on sampling.
I point to a variation of 'Importance Sampling' in Sampling theory would most likely constitute an inconsistent but improved estimator of the sample mean, where the correct percentage weighting of this class is not known (or, the subject of investigation), but it itself, is selected as 'the best available estimate'.
For example, take a poor country where a large percent of the population do not have bank accounts. Assume you were given access to spending data for those with accounts to develop figures for the nation as a whole. This would clearly represent closely the actual countries spending pattern, but because of the precise impact of unreported cash income and differing spending among those without bank accounts, this is not expected to completely 'consistent' with the countries actual total domestic spending.
The large size weighting of those with bank accounts clearly still makes it superior, albeit distorted, over the sampling variance expected in a simple random strategy scheme. Note, no matter how precisely one gathers the samples in the 'Importance Sampling' strata alone (so mathematically the estimate converges in probability to the this class's true value), it still remains inconsistent estimator for the parent population (as limitations on out-of-class sampling implies it cannot converges in probability to produce a combined estimator for the parent populations mean).
I can't comment, so I will add this as an answer. Whuber answer is just showing that one specific inconsistent estimator can be better than another specific consistent estimator. Since the questions was: "are there examples of an inconsistent estimator which outperforms a reasonable consistent estimator for all finite n" then of course his answer is ok.
However, this answer may give readers the impression that one needs to use an inconsistent estimator, and this is clearly not the case here.
For instance, in Whuber's case we can then take the estimator to be the upper end of a confidence interval, which will only underestimate the true mean at a chosen significance level, and thus will be superior to the mean itself. This estimator is still consistent, since the upper end of the confidence interval converges to the true $\mu$ as the sample size increases.
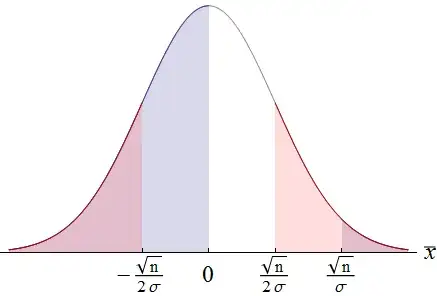
More specifically, are there examples of an inconsistent estimator which outperforms a reasonable consistent estimator for all finite n (with respect to some suitable loss function)?
Yes there are, and probably are more simpler and usual than you think. Moreover complex or unusual loss functions are not needed about that, usual MSE is enough.
The crucial concept here is bias-variance trade-off. Even in simple linear models setting, the wrong/misspecified model, that involve biased and inconsistent estimators for parameters and entire function, can be better then the correct one if our goal is prediction. Now, prediction is very relevant in real world.
The example is simple, you can think about a true model like this:
$y = \beta_1 x_1 + \beta_2 x_2 + \epsilon$
you can estimate several linear regression; a short like this:
$y = \theta_1 x_1 + u$
or longer that can also represent the empirical counterpart of true model. Now, the short regression is wrong (involve inconsistent and biased parameters and function) however is not sure that the longer (consistent) is better for prediction (MSE loss). Note that this story hold precisely in finite sample scheme, as you requested. Not asymptotically.
My point is clearly and exhaustively explained in: Shmueli - To explain or to predict - Statistical Science 2010, Vol. 25, No. 3, 289–310.
EDIT. For clarification I add something that, I hope, can be useful to the readers. I use, as in the article cited, the concept of bias in quite general way. It can be spent in both case: unbiased and consistent estimators. These two things different but the story above hold in both case. From now I speak about bias and we can spend it against consistency also (so, biased estimators = inconsistent estimators). The concept of bias are usually refers on parameters (let me refers on Wikipedia: https://en.wikipedia.org/wiki/Consistent_estimator#Bias_versus_consistency; https://en.wikipedia.org/wiki/Bias_of_an_estimator. However is possible to spend it more in general also. Suffice to say that not all estimated statistical models (say $f$) are parametric but all them can be biased in comparison to the true models (say $F$). Maybe in this way we can conflate consistency and misspecification problems but in my knowledge these two can be viewed as two face of the same coin.
Now the short estimated model (OLS regression) above $f_{short}$ is biased in comparison to the related true model $F$. Otherwise we can estimate another regression, say $f_{long}$ where all correct dependent variables are included, and potentially others are added. So $f_{long}$ is a consistent estimator for $F$. If we estimate $f_{true}$ where all and only the correct dependent variables are included we stay in the best case; or at least it seem so. Often this is the paradigm in econometrics, the field where I’m more confident. However in Shmueli (2010) is pointed out that explanation (causal inference) and prediction are different goals even if often them are erroneously conflated. Infact, at least if $n$ is finite, ever in practice, $f_{short}$ can be better than $f_{true}$ if our goal is prediction. I cannot give you an actual example here. The favourable conditions are listed in the article and also in this related and interesting question (Paradox in model selection (AIC, BIC, to explain or to predict?)); them come from an example like above.
Let me note that, until a few years ago, in econometrics literature this fact (bias-variance story) was highly undervalued but in machine learning literature is not the case. For example LASSO and RIDGE estimators, absent in many general econometrics textbooks but usual in machine learning ones, make sense primarily because the story above hold. Moreover we can consider parameters perspective also. In the example above $\theta_1$ come from the short regression and, taking apart few special cases, is biased in comparison to $\beta_1$. This fact come from the omitted variable bias story, that is an classic argument in any econometric textbooks. Now if we are precisely interested in $\beta$s this problem must be resolved but for prediction goals non necessarily. In the last case $f_{short}$ and therefore $\theta_1$ can be better than consistent estimators, therefore $f_{true}$ and its parameters.
Now we have to face a nuisance question. Consistency is an asymptotic property, however this not mean that we can speak about consistency only in theoretical case where we have $n=\inf$. Consistency, in any form, is useful in practice only because if $n$ is large we can say that this property hold. Unfortunately in most case we do not have a precise number for $n$ but sometimes we have an idea. Frequently consistency is simply viewed as weaker condition than unbiasedness, because in many practical case unbiased estimators are also consistent ones. In practice we often can speak about consistency and not about unbiased because the former can to hold and the last surely not, in econometrics it is almost always so. However, also in these case, is absolutely not the case that bias-variance trade-off, in the sense above, disappear. Idea like this is precisely the ones that leave us in dramatic errors that Shmueli (2010) underscore. We have to remember that $n$ can be large enough for some things and not for others, in the same model also. Usually we know nothing about that.
Last point. Bias-variance story, referred on usual MSE loss, can be spent also in another direction that is completely focused on parameters estimation. Any estimator have his mean and variance. Now, if an estimator is biased but have also lower variance than a competitor that is unbiased and/or consistent, is not obvious what is better. There is exactly a bias-variance trade-off, as explained in: Murphy (2012) - Machine Learning: A Probabilistic Perspective; pag 202.
