Calculate moments of a weighted mixture of normal distributions?

Question

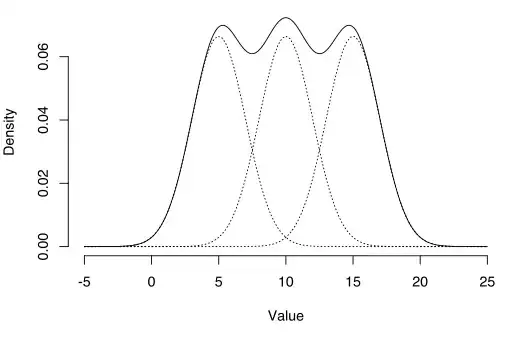
Lets say I have a bunch of dogs of different breeds $i = 1, 2, ..., n$. The probability of a random dog being of breed $i$ is $p_i$. The weight (in kg) of a dog of breed $i$ is $N(\mu_i, \sigma_i^2)$. How do I calculate the variance, skewness and kurtosis of the distribution of the weight of a random dog from a random breed?

Or, put differently, how do I calculate the variance, skewness and kurtosis for a weighted sum of normal distributions? Can it be done mathematically or do I need to use a Monte Carlo method?

Answer 1

Your model is that $(X|Y=i) \sim N(\mu_i,\sigma_i^2)$ and that $P(Y=i)=w_i$.

Using the law of total expectation, the mean is $$ EX = EE(X|Y)=E\mu_Y=\sum_{i=1}^n w_i \mu_i. $$ Similarly, using the law of total variance, \begin{align} \operatorname{Var}X &=E\operatorname{Var}(X|Y) + \operatorname{Var}EX|Y \\&=E\sigma_Y^2 + \operatorname{Var}\mu_Y \\&=E\sigma_Y^2 + \operatorname{Var}\mu_Y \\&=\sum_{i=1}^n w_i \sigma_i^2 + \sum_{i=1}^n w_i \mu_i^2 - (\sum_{i=1}^n w_i \mu_i)^2. \end{align} Finally, the law of total cumulance for the third cumulant (equal to the third central moment), says that the third central moment is equal to the expected conditional third central moment (zero in this case), plus the third central moment of the conditional expectation, plus three times the covariance between the conditional expectation and variance, that is, \begin{align}\mu_3(X) &= E((X-EX)^3) \\&=\operatorname{E}(\mu_3(X\mid Y))+\mu_3(\operatorname{E}(X\mid Y)) +3\operatorname{cov}(\operatorname{E}(X\mid Y),\operatorname{var}(X\mid Y)) \\&=\mu_3(\mu_Y)+3 \operatorname{Cov}(\mu_Y,\sigma_Y^2). \end{align}

Answer 2

Your density function for the variable has a closed form, it is a mixture of gaussians. The density below shows the idea. The density function is not that complicated, in this case it's just 1/3rd of the original densities summed.

Integration this new form is actually not that hard. For example, the variance of a mixture is just a simple formula based on its components. But just approximating it with a large sample is also easy! Just sample a breed, sample from its weight. Do that 10000 times. The sample variance is probably pretty good. You could generate a couple of those sample variances as well to see if they converged to your satisfaction. Same for sample skewness and sample kurtosis.

EDIT Didn't even start properly thinking about just calculating the moments from the definition. I have become lazy because sampling is so easy. But the other answer is better. Or, if your ambition is to become as lazy as me, join the club of people who cannot derive properties but only simulate them, this is your answer!