Variance matrix with equal diagonal entries in PROC MIXED

Question

Is it possible to specify a variance matrix for the random effects in PROC MIXED with the only restriction that the diagonal entries are equal ? I took a look in the help and I have not found, but this seems strange because such a variance structure is rather natural in some applications.

(EDIT) Consider for instance such a dataset:

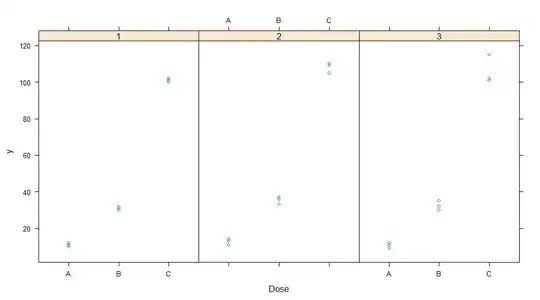
> dat
   Subject Dose   y
1        1    A  10
2        1    A  11
3        1    A  12
4        1    B  30
5        1    B  31
6        1    B  32
7        1    C 100
8        1    C 101
9        1    C 102
10       2    A  11
11       2    A  14
12       2    A  13
13       2    B  33
14       2    B  37
15       2    B  36
16       2    C 105
17       2    C 110
18       2    C 109
19       3    A   9
20       3    A  11
21       3    A  12
22       3    B  30
23       3    B  35
24       3    B  32
25       3    C 115
26       3    C 101
27       3    C 102

and the following model:

PROC MIXED DATA=dat ;
    CLASS SUBJECT DOSE ;
    MODEL y = DOSE ;
    RANDOM DOSE / subject=SUBJECT type=MYMATRIX ;
RUN; QUIT;

I want a matrix "MYMATRIX" with the same variance for each level of the DOSE factor, but not a compound symmetry matrix because the correlation between the means of the levels are different.

(EDIT2) The mathematical meaning of this model is the following one. Denoting by $i$ the index for the dose level and by $j$ the index for the subject, one has $$(y_{ijk} | \mu_{ij}) \sim_{\text{iid}} {\cal N}(\mu_{ij}, \sigma^2_w), \quad k=1, \ldots, 3 \quad \text{ for all } i,j$$ and $$ \begin{pmatrix} \mu_{1j} \\ \mu_{2j} \\ \mu_{3j} \end{pmatrix} \sim_{\text{iid}} {\cal N}_3 \left( \begin{pmatrix} \mu_1 \\ \mu_2 \\ \mu_3 \end{pmatrix}, G \right), \quad j=1, \ldots, 3$$ The diagonal entries of the $G$ matrix are the between variances for each level of the dose. I want $G$ to be of the form $$G=\begin{pmatrix} \sigma^2_b & \sigma_{12} & \sigma_{13} \\ \sigma_{12} & \sigma^2_b & \sigma_{23} \\ \sigma_{13} & \sigma_{23} & \sigma^2_b \end{pmatrix}$$

Answer 1

If I do understand your model, you have a random dose effect for each subject:

$$ \gamma = \left( \begin{array}{c} \gamma_{1A} \\ \gamma_{1B} \\ \gamma_{1C} \\ \gamma_{2A} \\ \gamma_{2B} \\ \gamma_{2C} \\ \gamma_{3A} \\ \gamma_{3B} \\ \gamma_{3C} \\ \end{array} \right), $$ and $G = \textrm{Var}(\gamma)$ has a block-diagonal structure with identical blocks over subjects: $$ G = \left( \begin{array}{ccc} \star & \star & \star & 0 & 0 & 0 & 0 & 0 & 0 \\ \star & \star & \star & 0 & 0 & 0 & 0 & 0 & 0 \\ \star & \star & \star & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & \star & \star & \star & 0 & 0 & 0 \\ 0 & 0 & 0 & \star & \star & \star & 0 & 0 & 0 \\ 0 & 0 & 0 & \star & \star & \star & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & \star & \star & \star \\ 0 & 0 & 0 & 0 & 0 & 0 & \star & \star & \star \\ 0 & 0 & 0 & 0 & 0 & 0 & \star & \star & \star \end{array} \right). $$

Now, the type option specifies the covariance structure of each block. If you specify type=vc (default) then each block will have the form $$ \left( \begin{array}{ccc} \star & \star & \star \\ \star & \star & \star \\ \star & \star & \star \end{array} \right) = \left( \begin{array}{ccc} \sigma_{_{G}}^{2} & 0 & 0 \\ 0 & \sigma_{_{G}}^{2} & 0 \\ 0 & 0 & \sigma_{_{G}}^{2} \end{array} \right), $$ where $\sigma_{_{G}}^{2}$ is the single parameter of $G$ to be estimated. If you specify type=toep then $$ \left( \begin{array}{ccc} \star & \star & \star \\ \star & \star & \star \\ \star & \star & \star \end{array} \right) = \sigma_{_{G}}^{2} \left( \begin{array}{ccc} 1 & \rho_1 & \rho_2 \\ \rho_1 & 1 & \rho_1 \\ \rho_2 & \rho_1 & 1 \end{array} \right), $$ and now there are three parameters in $G$ to be estimated.

$$$$

If this does not fit your requirement, then you might want to have a look at the group option: all observations having the same level of the group effect have the same covariance parameters.