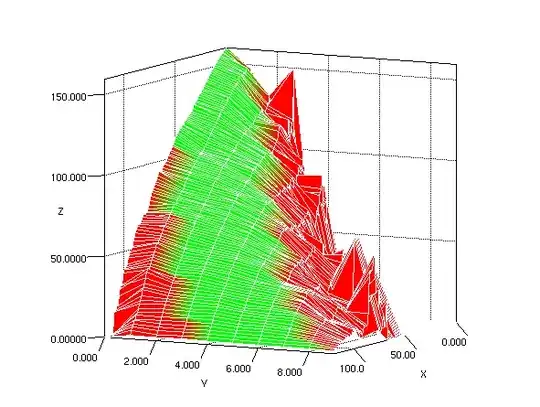
Hello I have many 3d points (x, y, z). I have averaged every z with a matching (x, y) value and plotted the resulting means as a surface.
The green indicates where the sample of points was greater than 100 i.e. the more reliable means.
What I want to do is construct a function z = f(x, y) which can take new (x, y) pairs and find where they should lie on the surface.
Having a look at the graph in  I can see the changing Y values have similar curves which look like they could be built as a function of Y.
I can see the changing Y values have similar curves which look like they could be built as a function of Y.
That makes me think that I should go about building the function z = Fy(x) where Fy is a function outputted by some g(y).
Is this possible? Can you create a function which outputs a new function? I suppose it could be a sort of parametric function taking in y and outputting x coefficients?
My brain is fried anyway, am I on the right lines?