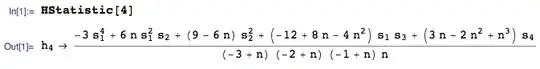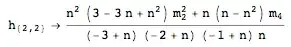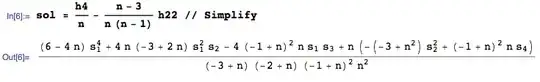The question is to find an unbiased estimator of:
$$\text{Var}(S^2)=\frac{\mu_4}{n}-\frac{(n-3)}{n(n-1)} {\mu_2^2}$$
... where $\mu_r$ denotes the $r^\text{th}$ central moment of the population. This requires finding unbiased estimators of $\mu_4$ and of $\mu_2^2$.
An unbiased estimator of $\mu_4$
By defn, an unbiased estimator of the $r^\text{th}$ central moment is the $r^\text{th}$ h-statistic: $$\mathbb{E}[h_r] = \mu_r$$
The $4^\text{th}$ h-statistic is given by:
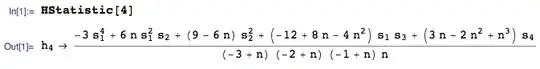where:
i) I am using the HStatistic function from the mathStatica package for Mathematica
ii) $s_r$ denotes the $r^\text{th}$ power sum $$s_r=\sum _{i=1}^n X_i^r$$
Alternative:
The OP asked about finding an unbiased solution in terms of sample central moments $m_r=\frac{1}{n} \sum _{i=1}^n \left(X_i-\bar{X}\right)^r$. An unbiased estimator of $\mu_4$ in terms of $m_i$ is:
An unbiased estimator of $\mu_2^2$
An unbiased estimator of a product of central moments (here, $\mu_2 \times \mu_2$)is known as a polyache (play on poly-h). An unbiased estimator of $\mu_2^2$ is given by:
where:
i) I am using the PolyH function from the mathStatica package for Mathematica
ii) For more detail on polyaches, see section 7.2B of Chapter 7 of Rose and Smith, Mathematical Statistics with Mathematica (am one of the authors), a free download of which is available here.
While mathStatica does not have an automated converter to express PolyH in terms of sample central moments $m_i$ (nice idea), doing that conversion yields:
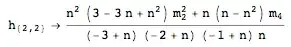
Putting it all together:
An unbiased estimator of $\frac{\mu_4}{n}-\frac{(n-3)}{n(n-1)} {\mu_2^2}$ is thus:
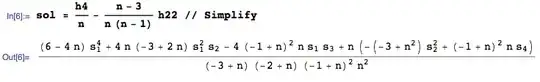
or, more compactly, in terms of sample central moments $m_i$:
........... 
And as a check, we can run the expectations operator over the above (the $1^\text{st}$ RawMoment of sol), expressing the solution in terms of Central moments of the population:
... and all is good.
