Percentiles of mixture distribution: negative values?

Question

I am trying to grasp what is the meaning of getting unexpected negative values for some percentiles of a mixture distribution. Let the distribution function pdf be:

\begin{equation} f(x) = (1-p)\cdot \delta(x) + p\cdot \lambda e^{-\lambda\,x} \cdot H(x) \end{equation} where $p$ is the probability of the value of $x$ being modeled as an exponential function and $(1-p)$ the probability of it being equal to zero. Also, $\textit{delta}$ and the $\textit{Heaviside step function}$ are the indicator functions of the intended supports.

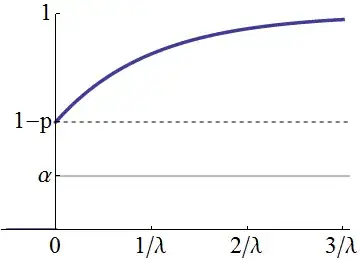
If we integrate $f(x)$ from 0 to C, where C is the value of of the $n_{th}$ percentile, we can express C as:

\begin{equation} C = \frac{ln(\frac{1-n_{th}}{p})}{-\lambda} \end{equation}

My question is: provided that the expression of C is correct, $C < 0$ whenever $(1-n_{th}) < p$.

Probably I am not properly deriving the expression of C, specially regarding the integration of the $\textit{delta}$ function. If that is not the case, what is the meaning of a negative valued percentile when the support of both distribution functions is greater than or equal to zero?

Answer 1

The meaning of "$\delta$" in $ f(x) = (1-p)\cdot \delta(x) + p\cdot \lambda e^{-\lambda\,x} \cdot H(x) $, as a "generalized function," is it is a quantity that when integrated against any continuous "test function" $g$ with compact support yields $g(0)$. (This differs from the indicator of zero, which when integrated against any test function yields only zero.) In particular,

$$\int_{-\infty}^x \delta(x)dx = \lim_{y\to x^{+}}\lim_{a\to-\infty}\int_a^y 1\delta(x)dx = \left\{\matrix{0 & x \lt 0 \\ 1 & x \ge 0}\right. = H(x).$$

(The left-hand limit as $y$ decreases to $x$ was taken in order to assure the left continuity of $F$. The technical problem it addresses concerns the fact that when $x=0$ we're trying to integrate a function equal to $1$ for non-positive $x$ and zero for positive $x$ and, unfortunately, that is not continuous at $0$. For any other $x\ne 0$, the limit over $y$ is superfluous.)

Through the usual rules of integration $f$ determines the distribution function

$$\eqalign{ F(x) &= \int_{-\infty}^x f(x) dx = (1-p)\int_{-\infty}^x \delta(x)dx + p\lambda\int_{-\infty}^x e^{\lambda x}H(x) dx\\ &=(1-p)H(x) + p\lambda \int_0^{\max(0,x)} e^{-\lambda x}dx\\ &=(1-p)H(x) + p \left(1 - e^{-\lambda\max(0,x)}\right). }$$

Given a number $0\lt \alpha\le 1$, the solution to $F(x)=\alpha$ is obtained by considering whether $\alpha \lt 1-p$ or $\alpha \ge 1-p$, as suggested by this generic graph of $F$ (the thick blue curve with a jump at zero):

Obviously, zero ought to be the $\alpha$ percentile for $F$ whenever $0\le \alpha\lt 1-p$. Since $$F(0)=(1-p)H(0) +p (1 - e^0) = 1-p \gt \alpha$$ and $$F(x)=0 \le \alpha$$ for all $x\lt 0$, $x=0$ indeed satisfies the requirements to be an $\alpha$ quantile. For $\alpha \ge 1-p$, the equation

$$\alpha = F(x) = (1-p) + p(1 - e^{-\lambda x}) = 1 - p e^{-\lambda x}$$

has the unique solution

$$F^{-1}(\alpha) = x = -\frac{1}{\lambda}\log\left(\frac{1-\alpha}{p}\right) \ge 0$$

as given in the question.

In no case, with positive $\alpha$, is there a solution $F(x)=\alpha$ for which $x$ is negative.

Answer 2

It looks like your distribution function is incorrect. First of all, you have to be careful when defining a mixed-density. It's natural to give a definition for an arbitrary probability mass function or density function. But when your random variable is mixed, there is no easy way to express that. The best solution is to define the cumulative distribution function as that's a well-defined quantity for any arbitrary random variable. In your case, the CDF would have the form: $$ F(x) = (1 - p) I(x \ge 0) + p (1 - \exp(-\lambda x)) $$ Note that this function isn't differentiable at zero so it doesn't correspond to the expression you gave. However, you can use this function to derive the associated quantile function. It is given by $$ F^{-1}(y) = -\dfrac 1 \lambda \ln\bigg(\dfrac {1 - y} p\bigg) I(y \ge p)$$ If the quantile of interest, $y$, is less than $p$, then the quantile function is equal to zero.

*Correction: The quantile function above is incorrect due to the indicator function. The correct formula is $$ F^{-1}(y) = -\dfrac 1 \lambda \ln\bigg(\dfrac {1 - y} p\bigg) I(y \ge 1 - p)$$ Also, the formula for the CDF above requires implicit multiplication by an indicator function as given below: $$ F(x) = [(1 - p) + p (1 - \exp(-\lambda x))] I(x \ge 0) $$