Probability of k zeros give the sum of n Poisson random variables is t?

Question

Suppose that I have $X_1,X_2,X_3,...X_n$ iid random variables from a Poisson distribution of parameter $\lambda$. Given that $X_1 +X_2+X_3 +...+X_n = t$, what is the probability that exactly $k$ of $X_1,X_2,X_3,...X_n$ are zero?

--

My approach: I started out by considering the joint probability mass function where $X_1 +X_2+X_3 +...+X_n = t$ and $k$ of $X_1,X_2,X_3,...X_n$ is zero but I do not know how to proceed from here. If I use a binomial model to calculate the probability of having k number of zeros, I do not know how to impose the constraint on the sum of $X_n$.

Answer 1

$Y = X_1+X_2+\cdots + X_n$ is a Poisson random variable with parameter $n\lambda$. So you can write down an expression for $P(Y=t)$.

There are $\binom{n}{k}$ choices for a set of $k$ variables that are zero. Pick a specific set. Then, the sum of the complementary set of variables is a Poisson random variable $Z$ with parameter $(n-k)\lambda$, and $Z$ is independent of the chosen $k$ variables. So, you can use independence to write down expressions for

$P(Z=t)$,

$P($chosen $k$ variables are $0)$,

$P($chosen $k$ are zero AND $Z=t) = P($chosen $k$ are zero AND $Y=t)$.

Can you take it from here? There shouldn't be any binomial distributions involved...

Answer 2

Let $Y:=X_1+\ldots+X_n$. Observe that the distribution of $(X_1,\ldots,X_n)$ conditional on $Y = t$ is multinomial (exercise). This gives a conceptually easier way to think about the problem- you have $n$ boxes and throw $t$ balls in them at random. What is the probability that $k$ are empty?

Well, first of all, there are $n^t$ ways of throwing the $t$ balls in the $n$ boxes with no restrictions.

Now it gets a little more complicated, even though we are just counting stuff. There are $\binom{n}{k}$ ways of choosing the $k$ boxes that stay empty. We are then left with $t$ balls to throw into the $n-k$ remaining boxes, such that each box is not empty. You can do this by inclusion/exclusion, just like in the proof of the Stirling number https://math.stackexchange.com/questions/550256/stirling-numbers-of-second-type .

Combining these ingredients gives the desired probability, $$ \frac{1}{n^t}\binom{n}{k}\sum_{j=0}^{n-k} (-1)^{n-k-j} \binom{n-k}{j} j^t, $$ $t \ge n-k$, $n \ge k$.

Note that $\lambda$ does not feature in the answer.

---

Out of interest and as a quick exercise I coded this (borrowing a Stirling number function I found with Google) to see what the answer looks like:

##-- Stirling numbers of the 2nd kind
##-- (Abramowitz/Stegun: 24,1,4 (p. 824-5 ; Table 24.4, p.835)

##> S^{(m)}_n = number of ways of partitioning a set of $n$ elements into $m$
##> non-empty subsets

Stirling2 <- function(n,m)
{
  ## Purpose:  Stirling Numbers of the 2-nd kind
  ##        S^{(m)}_n = number of ways of partitioning a set of
  ##                      $n$ elements into $m$ non-empty subsets
  ## Author: Martin Maechler, Date:  May 28 1992, 23:42
  ## ----------------------------------------------------------------
  ## Abramowitz/Stegun: 24,1,4 (p. 824-5 ; Table 24.4, p.835)
  ## Closed Form : p.824 "C."
  ## ----------------------------------------------------------------

  if (0 > m || m > n) stop("'m' must be in 0..n !")
  k <- 0:m
  sig <- rep(c(1,-1)*(-1)^m, length= m+1)# 1 for m=0; -1 1 (m=1)
  ## The following gives rounding errors for (25,5) :
  ## r <- sum( sig * k^n /(gamma(k+1)*gamma(m+1-k)) )
  ga <- gamma(k+1)
  round(sum( sig * k^n /(ga * rev(ga))))
}


pmf<-function(n,t,k) {
  if (t >= (n-k) & n >= k) {
    (choose(n,k) * factorial(n-k) * Stirling2(t,n-k) )/(n^t)
  } else {
    0
  }
}


lambda <- 1
n <- 10
reps <- 500000
set.seed(2017)
X <- matrix(ncol=n,nrow=reps,data=rpois(n*reps,lambda))

K <- apply(X, 1,function(x){sum(x == 0)})
hist(K)

# restrict only to those that sum to t
Y<-rowSums(X)


t<-8
G<- (Y == t)
sum(G)

k <- 5
#head(X[which(K==k),])
#head(Y[which(K==k)])
#head(X[G,])
#head(Y[G])

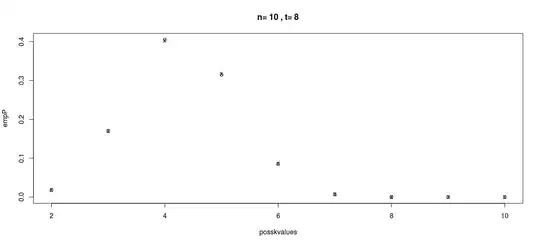
posskvalues <- (n-t):n
nk <- length(posskvalues)
empP <- numeric(nk)
thP <- numeric(nk)

for(i in 1:nk) {
  k <- posskvalues[i]
# sum(K[G] == k)
  empP[i] <- sum(K[G] == k)/sum(G)
  thP[i] <- pmf(n,t,k)
}

plot(posskvalues,empP,main=paste("n=",n,", t=",t))
points(posskvalues,thP,pch="x")